Щ…ЩҶ ШЁШұШ§ЫҢ Щ…Ш№Ш§ШҜЩ„ЩҮ $\sin x=x$ ШӘЩҲШ¶ЫҢШӯШ§ШӘЫҢ Щ…ЫҢШҜЩ… .ЪҶЩҶЫҢЩҶ Щ…Ш№Ш§ШҜЩ„Ш§ШӘЫҢ ШұШ§ ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ ШұЩҲШҙ ШўЩҶШ§Щ„ЫҢШІЫҢ Ш¬ЩҲШ§ШЁЫҢ ШЁШұШ§ЫҢШҙ ЫҢШ§ЩҒШӘ. ШҜШұ Ш§ЫҢЩҶ ЪҜЩҲЩҶЩҮ Щ…Ш№Ш§ШҜЩ„Ш§ШӘ ШЁШ§ЫҢШҜ ЫҢШ§ Ш§ШІ ШұЩҲШҙ ЩҮЩҶШҜШіЫҢ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢШҜ ЫҢШ§ Ш§ШІ ШұЩҲШҙ ЩҮШ§ЫҢ Ш№ШҜШҜЫҢ Ъ©Щ…Ъ© ШЁЪҜЫҢШұЫҢШҜ ЩҲ ШӘЩӮШұЫҢШЁЫҢ Ш§ШІ Ш¬ЩҲШ§ШЁ ШұШ§ ШЁЩҮ ШҜШіШӘ Ш§ЩҲШұЫҢШҜ.
ШЁШұШ§ЫҢ ШұЩҲШҙ ЩҮЩҶШҜШіЫҢ :
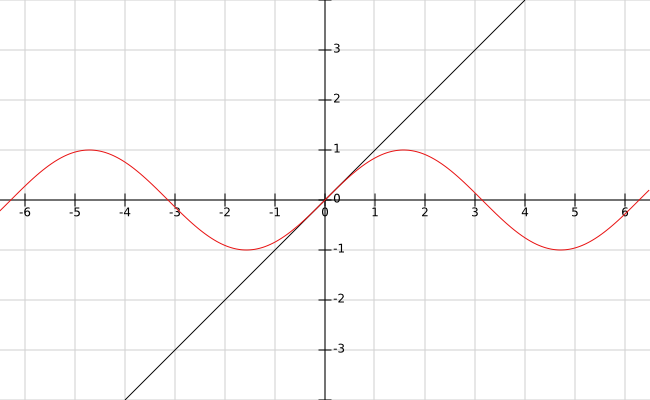
ЩҲШ§Ш¶Шӯ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ© Ш¬ЩҲШ§ШЁ ШҜШ§ШұШҜ ЩҲ Ш¬ЩҲШ§ШЁ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $x=0$ .
Ш§Щ…Ш§ ШЁШұШ§ЫҢ ЫҢШ§ЩҒШӘЩҶ ШӘЩӮШұЫҢШЁЫҢ Ш§ШІ Ш¬ЩҲШ§ШЁ Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢШҜ Ш§ШІ ШұЩҲШҙ ЩҮШ§ЫҢ Ш№ШҜШҜЫҢ Ш§ШІ Ш¬Щ…Щ„ЩҮ ШұЩҲШҙ Щ…Ш№ШұЩҲЩҒ ШӘЩӮШұЫҢШЁ ЩҶЫҢЩҲШӘЩҶ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢШҜ (Ш§ЫҢЩҶШ¬Ш§ ШұШ§ ШЁШЁЫҢЩҶЫҢШҜ)
ЩӮШұШ§Шұ ШҜЩҮЫҢШҜ $f(x)=x-\sin x=0$
ШЁШ§ ЫҢЪ© ШӯШҜШі Ш§ЩҲЩ„ЫҢЩҮ $x_0$ Ъ©ЩҮ ЩҒЪ©Шұ Щ…ЫҢЪ©ЩҶЫҢЩ… ЩҶШІШҜЫҢЪ© ШЁЩҮ Ш¬ЩҲШ§ШЁ ШЁШ§ШҙШҜ ШҙШұЩҲШ№ Щ…ЫҢ Ъ©ЩҶЫҢЩ… ЩҲ $x_1$ ШұШ§ Ш§ШІ ШұШ§ШЁШ·ЩҮ ЫҢ $$x_1=x_0-\frac{f(x_0)}{f'(x_0)}$$ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұЫҢЩ…. ШҜШұ ЩҲШ§ЩӮШ№ $x_1$ Ш§ЫҢЩҶШ·ЩҲШұ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ: Щ…Ш№Ш§ШҜЩ„ЩҮ Ш®Ш· Щ…Щ…Ш§Ші ШЁШұ ЩҶЩ…ЩҲШҜШ§Шұ ШӘШ§ШЁШ№ $f$ ШұШ§ ШҜШұ ЩҶЩӮШ·ЩҮ $x_0$ ЩҶЩҲШҙШӘЩҮ ЩҲ $x_1$ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ЩҶЩӮШ·ЩҮ Ш§ЫҢ Ъ©ЩҮ Ш§ЫҢЩҶ Ш®Ш· Щ…Щ…Ш§Ші Щ…ШӯЩҲШұ $x$ ЩҮШ§ ШұШ§ ЩӮШ·Ш№ Ъ©ШұШҜЩҮ Ш§ШіШӘ. ШӯШ§Щ„ $x_1$ ШұШ§ ЩҶЩӮШ·ЩҮ Ш¬ШҜЫҢШҜ ЪҜШұЩҒШӘЩҮ ЩҲ Щ…ШұШӯЩ„ЩҮ ЩӮШЁЩ„ ШұШ§ ШӘЪ©ШұШ§Шұ Щ…ЫҢ Ъ©ЩҶЫҢЩ…. ЫҢШ№ЩҶЫҢ Щ…Ш№Ш§ШҜЩ„ЩҮ Ш®Ш· Щ…Щ…Ш§Ші ШЁШұ ЩҶЩ…ЩҲШҜШ§Шұ $f$ ШҜШұ ЩҶЩӮШ·ЩҮ $x_1$ ШұШ§ Щ…ЫҢ ЩҶЩҲЫҢШіЫҢЩ… ЩҲ Ш§ЫҢЩҶ Ш®Ш· Щ…Щ…Ш§Ші ЩҮШұ Ш¬Ш§ ЩҶЩ…ЩҲШҜШ§Шұ $x$ ЩҮШ§ ШұШ§ ЩӮШ·Ш№ Ъ©ШұШҜ $x_2$ Щ…ЫҢ ЩҶШ§Щ…ЫҢЩ…. ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ ШЁЩҮ ЫҢЪ© ШҜЩҶШЁШ§Щ„ЩҮ
$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ Щ…ЫҢ ШұШіЫҢЩ…. Ш§ЫҢЩҶ ШҜЩҶШЁШ§Щ„ЩҮ ШЁЩҮ ШіЩ…ШӘ ШұЫҢШҙЩҮ ЫҢ Ш§ЫҢЩҶ Щ…Ш№Ш§ШҜЩ„ЩҮ Щ…ЫҢЩ„ Щ…ЫҢ Ъ©ЩҶШҜ.
(ШҜШұ ШҙЪ©Щ„ ШІЫҢШұ ШұЩҲШҙ ЩҶЫҢЩҲШӘЩҶ ЩҶЩ…Ш§ЫҢШҙ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ. ШҙЪ©Щ„ Ш§ШІ ЩҲЫҢЪ©ЫҢ ЩҫШҜЫҢШ§)

ШұЩҲШҙ ШҜЫҢЪҜШұ Ъ©ЩҮ ЩҶШҙШ§ЩҶ Щ…ЫҢ ШҜЩҮШҜ ШҜШұ ЫҢЪ© ШЁШ§ШІЩҮ Ш§ЫҢ ШўЫҢШ§ Щ…Ш№Ш§ШҜЩ„ЩҮ $f(x)=0$ ШұЫҢШҙЩҮ ШҜШ§ШұШҜ ЫҢШ§ Ш®ЫҢШұ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ЩӮШ¶ЫҢЩҮ ШЁЩҲЩ„ШІШ§ЩҶЩҲ Ш§ШіШӘ:
ЩӮШ¶ЫҢЩҮ: Ш§ЪҜШұ ШӘШ§ШЁШ№ $f:[a,b]\to\mathbb R$ ЩҫЫҢЩҲШіШӘЩҮ ШЁШ§ШҙШҜ ЩҲ $f(a)f(b)< 0$ ШўЩҶЪҜШ§ЩҮ ШӘШ§ШЁШ№ $f$ ШҜШұ ШЁШ§ШІЩҮ $(a,b)$ ШӯШҜШ§ЩӮЩ„ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШ§ШұШҜ.
ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ ЪҶЩҲЩҶ ШӘШ§ШЁШ№ $f(x)=x-\sin x$ ЩҫЫҢЩҲШіШӘЩҮ Ш§ШіШӘ Ш§ЪҜШұ ШўЩҶ ШұШ§ ШұЩҲЫҢ ШЁШ§ШІЩҮ $[-1,1]$ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢЩ… $f(-1)=-1-\sin(-10=-1+\sin 1<0$ ЩҲ $f(1)=1-\sin 1> 0$ ШЁЩҶШ§ШЁШұ Ш§ЫҢЩҶ Ш§ШІ ЩӮШ¶ЫҢЩҮ ШЁЩҲЩ„ШІШ§ЩҶЩҲ Ш«Ш§ШЁШӘ Щ…ЫҢ ШҙЩҲШҜ Щ…Ш№Ш§ШҜЩ„ЩҮ$f(x)=0$ ШҜШ§ШұШ§ЫҢ ШӯШҜШ§ЩӮЩ„ ЫҢЪ© ШұЫҢШҙЩҮ ШЁЫҢЩҶ $(-1,1)$ Ш§ШіШӘ. ЩҲ ЪҶЩҲЩҶ $f(x)=x-\sin x$ ШұЩҲЫҢ Ш§ЫҢЩҶ ШЁШ§ШІЩҮ Ш§Ъ©ЫҢШҜШ§ ШөШ№ЩҲШҜЫҢ Ш§ШіШӘ ЩҶШӘЫҢШ¬ЩҮ Щ…ЫҢЪҜЫҢШұЫҢЩ… ШҜЩӮЫҢЩӮШ§ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШұ Ш§ЫҢЩҶ ШЁШ§ШІЩҮ ШҜШ§ШұШҜ. Ш§ШІ Ш·ШұЩҒЫҢ ШЁШұШ§ЫҢ $x>1$ ЪҶЩҲЩҶ $x> \sin x$ Щ„Ш°Ш§ ШҜШұ ШЁШ§ШІЩҮ $(1,\infty)$ Щ…Ш№Ш§ШҜЩ„ЩҮ Ш¬ЩҲШ§ШЁ ЩҶШҜШ§ШұШҜ ЩҲ ШЁШұШ§ЫҢ ШЁШ§ШІЩҮ $x< -1$ ЪҶЩҲЩҶ $x< \sin x$ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШҜШұ ШЁШ§ШІЩҮ $(-\infty,-1)$ ЩҮЩ… Ш¬ЩҲШ§ШЁ ЩҶШҜШ§ШұШҜ. ЩҫШі Ш§ЫҢЩҶ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜЩӮЫҢЩӮШ§ ЫҢЪ© Ш¬ЩҲШ§ШЁ ШҜШ§ШұШҜ ЩҲ ШўЩҶ ЩҮЩ… ШҜШұ ШЁШ§ШІЩҮ $(-1,1)$ Ъ©ЩҮ ЩҮЩ…Ш§ЩҶШ·ЩҲШұ Ъ©ЩҮ ЩҲШ§Ш¶Шӯ Ш§ШіШӘ $x=0$ Ш¬ЩҲШ§ШЁ Ш§ШіШӘ.
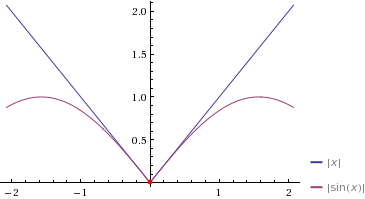
ШҜШұ Щ…ЩҲШұШҜ Щ…Ш№Ш§ШҜЩ„ЩҮ $|x|=|\sin x|$ ЪҶЩҲЩҶ $|\sin 0|=|0|=0$ Щ„Ш°Ш§ ШҜШұ ШөЩҒШұ ШЁШұШ§ШЁШұЩҶШҜ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҙЪ©Щ„ ШӘЩҶЩҮШ§ Ш¬ЩҲШ§ШЁ ЩҮЩ…ЫҢЩҶ ШөЩҒШұ Ш§ШіШӘ.