Ш§ЩҲЩ„Ш§ Ъ©ЩҮ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ЩҶШӘШёЩ… ШұШ§ Щ…ЫҢШӘЩҲШ§ЩҶ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШӘШ№ШҜШ§ШҜ Ш¶Щ„Ш№ ШЁЩҮ ШҜЩҲ ШҜШіШӘЩҮ ШІЫҢШұ ШӘЩӮШіЫҢЩ… Ъ©ШұШҜ:
(Ш§Щ„ЩҒ) ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҒШұШҜ Ш¶Щ„Ш№
(ШЁ) ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ШІЩҲШ¬ Ш¶Щ„Ш№
ШҜШұ Щ…ЩҲШұШҜ (Ш§Щ„ЩҒ) ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ЩҶШҜШ§ШұШҜ .(Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ЩҶЩӮШ·ЩҮ Ш§ЫҢ Ш§ШіШӘ Ъ©ЩҮ Ш§ЪҜШұ ЩҮШұ ЩҶЩӮШ·ЩҮ ШұЩҲЫҢ Щ…ШӯЫҢШ· ШҙЪ©Щ„ ШұШ§ ШЁЩҮ ШўЩҶ ЩҲШөЩ„ Ъ©ШұШҜЩҮ ЩҲ Ш§ШІ Ш·ШұЩҒ ШҜЫҢЪҜШұ ШЁЩҮ ЩҮЩ…Ш§ЩҶ Ш§ЩҶШҜШ§ШІЩҮ Ш§ШҜШ§Щ…ЩҮ ШҜЩҮЫҢЩ… ЩӮШұЫҢЩҶЩҮ ШўЩҶ ЩҶЫҢШІ ШұЩҲЫҢ Щ…ШӯЫҢШ· ШЁЫҢЩҒШӘШҜ)
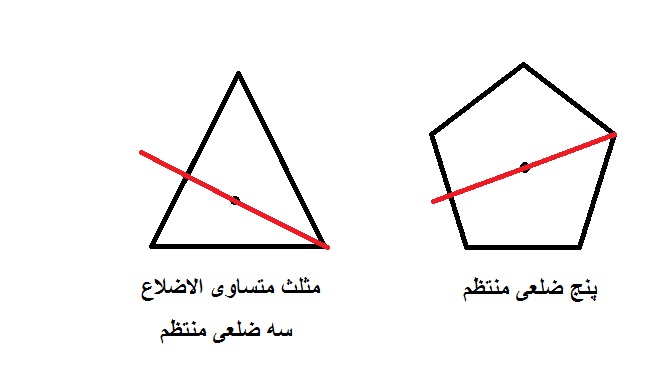
ШҜШұ Щ…ЩҲШұШҜ (ШЁ) ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ЫҢЪ© Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ШҜШ§ШұШҜ Ъ©ЩҮ ШўЩҶ ЩҮЩ… Щ…ШӯЩ„ ШЁШұШ®ЩҲШұШҜ ЩӮШ·ШұЩҮШ§ЫҢЫҢ Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ ШЁШұШ®ЩҲШұШҜ ЩӮШ·Шұ ШұШ§Ші ЩҮШ§ЫҢЫҢ Ъ©ЩҮ ЩҒШ§ШөЩ„ЩҮ ШўЩҶЩҮШ§ Ш§ШІ ЩҮЩ… ЩҶШөЩҒ ШӘШ№ШҜШ§ШҜ Ш¶Щ„Ш№ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Ш§ШіШӘ ЩҫШҜЫҢШҜ Щ…ЫҢ ШўЫҢШҜ.
 ЩҫШі:
Ш¬ЩҲШ§ШЁ Ш§Щ„ЩҒ) ШҜШұ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ Ш¶Щ„Ш№ ШІЩҲШ¬ Ш·ШЁЩӮ ШҙЪ©Щ„ ШЁШ§Щ„Ш§ ЩҒЩӮШ· ЩӮШ·ШұЩҮШ§ЫҢЫҢ Ш§ШІ Щ…ШұЪ©ШІ(Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ) Ш№ШЁЩҲШұ Щ…ЫҢЪ©ЩҶЩҶШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„ЩҮ ШўЩҶ ШұШ§Ші ЩҮШ§ ЩҶШөЩҒ ШӘШ№ШҜШ§ШҜ Ш§Ш¶Щ„Ш§Ш№ ШЁШ§ШҙШҜ ЩҲ ШЁЩӮЫҢЩҮ Ш®ЫҢШұ.
ШҜШұ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҒШұШҜ Ш¶Щ„Ш№ ЪҶЩҲЩҶ Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШұШҜ ЩҫШі ЩҮЫҢЪҶ ЩӮШ·ШұЫҢ Ш§ШІ Щ…ШұЪ©ШІ ШўЩҶ Ш№ШЁЩҲШұ ЩҶЩ…ЫҢЪ©ЩҶШҜ.
ЩҫШі:
Ш¬ЩҲШ§ШЁ Ш§Щ„ЩҒ) ШҜШұ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ Ш¶Щ„Ш№ ШІЩҲШ¬ Ш·ШЁЩӮ ШҙЪ©Щ„ ШЁШ§Щ„Ш§ ЩҒЩӮШ· ЩӮШ·ШұЩҮШ§ЫҢЫҢ Ш§ШІ Щ…ШұЪ©ШІ(Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ) Ш№ШЁЩҲШұ Щ…ЫҢЪ©ЩҶЩҶШҜ Ъ©ЩҮ ЩҒШ§ШөЩ„ЩҮ ШўЩҶ ШұШ§Ші ЩҮШ§ ЩҶШөЩҒ ШӘШ№ШҜШ§ШҜ Ш§Ш¶Щ„Ш§Ш№ ШЁШ§ШҙШҜ ЩҲ ШЁЩӮЫҢЩҮ Ш®ЫҢШұ.
ШҜШұ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҒШұШҜ Ш¶Щ„Ш№ ЪҶЩҲЩҶ Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШұШҜ ЩҫШі ЩҮЫҢЪҶ ЩӮШ·ШұЫҢ Ш§ШІ Щ…ШұЪ©ШІ ШўЩҶ Ш№ШЁЩҲШұ ЩҶЩ…ЫҢЪ©ЩҶШҜ.
Ш¬ЩҲШ§ШЁ ШЁ)ШҜШұ Щ…ЩҲШұШҜ ЩӮШ·ШұЩҮШ§ЫҢ ЩҶЫҢЩ…ШіШ§ШІ ЩҮЩ… ШҜЩӮЫҢЩӮШ§ ЩҮЩ…Ш§ЩҶ Ш¬ЩҲШ§ШЁ Ш§Щ„ЩҒ Ш§ШіШӘ Щ…ЩҶШӘЩҮШ§ ШЁШұШ§ЫҢ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҒШұШҜ Ш¶Щ„Ш№ Ш№Щ…ЩҲШҜ Щ…ЩҶШөЩҒ ЩҮШ§ЫҢЫҢ Ъ©ЩҮ Ш§ШІ ЩҮШұ ШұШ§Ші ШЁШұ Ш¶Щ„Ш№ Щ…ЩӮШ§ШЁЩ„ ШұШіЩ… ШҙЩҲШҜ ЩҶЫҢЩ…ШіШ§ШІ ЩҮЩ… Щ…ЫҢШҙЩҲЩҶШҜ.
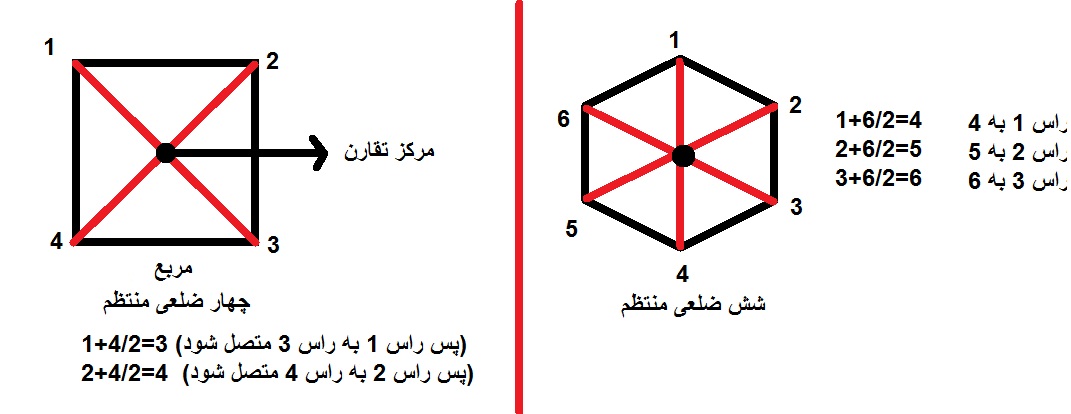
Ш¬ЩҲШ§ШЁ Щҫ) ШӘШ№ШҜШ§ШҜ Щ…ШӯЩҲШұ ШӘЩӮШ§ШұЩҶ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ( ШЁШҜЩҲЩҶ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШӘШ№ШҜШ§ШҜ Ш§Ш¶Щ„Ш§Ш№) ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ ШӘШ№ШҜШ§ШҜ Ш¶Щ„Ш№ ЩҮШ§. Щ…Ш«Щ„Ш§ ШіЩҮ Ш¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШіЩҮ Щ…ШӯЩҲШұ ШӘЩӮШ§ШұЩҶ ЩҲ ЪҶЩҮШ§Шұ Ш¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ЪҶЩҮШ§Шұ Щ…ШӯЩҲШұ ШӘЩӮШ§ШұЩҶ ШҜШ§ШұШҜ.
Ш¬ЩҲШ§ШЁ Ш¬ ЩҲ ЪҶ) Ш§ЪҜШұ Щ…ЩҶШёЩҲШұ Ш§ШІ Щ…ШұЪ©ШІ ШҢ Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ШЁШ§ШҙШҜ ШЁШұШ§ЫҢ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ЩҶШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҒШұШҜ Ш¶Щ„Ш№ Ъ©ЩҮ Щ…ШұЪ©ШІ ШӘШ№ШұЫҢЩҒ ЩҶЩ…ЫҢШҙЩҲШҜ ЩҫШі ШөШӯШЁШӘ Ш§ШІ ЩҒШ§ШөЩ„ЩҮ ЩҮЩ… ШЁЫҢ Щ…Ш№ЩҶЫҢ Ш§ШіШӘ ЩҲЩ„ЫҢ ШҜШұ Щ…ЩҲШұШҜ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ЩҮШ§ЫҢ Щ…ШӘШёЩ… ШЁШ§ ШӘШ№ШҜШ§ШҜ ШІЩҲШ¬ Ш¶Щ„Ш№ Ш·ШЁЩӮ ШӘШ№ШұЫҢЩҒ Щ…ШұЪ©ШІ ШӘЩӮШ§ШұЩҶ ШЁЩ„ЩҮ ЩҒШ§ШөЩ„ЩҮ Щ…ШұЪ©ШІ ШӘШ§ ШұШ§Ші ЩҮШ§ ЩҲ ЩҒШ§ШөЩ„ЩҮ Щ…ШұЪ©ШІ ШӘШ§ Ш¶Щ„Ш№ ЩҮШ§ ШЁЩҶШ§ШЁШұ ЩҮЩ…ЩҶЩҮШҙШӘЫҢ Щ…Ш«Щ„Ш« ЩҮЩ…ЪҜЫҢ ШЁШұШ§ШЁШұ Ш§ШіШӘ.