کوهن مکالی است از آنجایی که کردال است و برای گرافهای کردال کافیه $ unmixed $ باشند که به وضوح چنین است(تنها مجموعه پوشش راسی مینیمال آن مجموعه های $\{1,3\} $و$\{2,4\} $هستند)
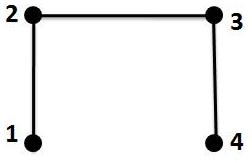
اما این گراف را میتوان به صورت زیر نگاه کرد که در این صورت یک گراف دوبخشی است(برای هماهنگی با قضیه $9.1.14$ آن را به صورت زیر نمایش میدهیم)
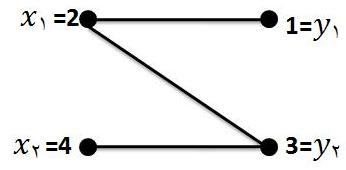
در حالت کلی نمیتوان از روی ظاهر کوهن مکالی بودن گرافها را تشخیص داد اما قضایایی نظیر $9.3.14$و $9.1.14$ برای حالت های خاص ابزارهایی را به ما میدهند.
مثلا در کردالها کافیه $ unmixed $ باشند یعنی تمام مینیمال پوشش راسی ها دارای یک کاردینالیتی باشند.