ШӯЩӮЫҢЩӮШӘШҙ Щ…ЩҶ Ш§ЩҲЩ„ЫҢЩҶ ШЁШ§ШұЩҮ Ъ©ЩҮ Ш§ШіЩ… Ш§ЫҢЩҶ ЩӮШ¶ЫҢЩҮ ШұЩҲ ШҙЩҶЫҢШҜЩ… ЩҲ ЩҲЩӮШӘЫҢ ШіШұЪҶ Ъ©ШұШҜЩ… Ш§ЫҢЩҶЩҲ ЩҫЫҢШҜШ§ Ъ©ШұШҜЩ…: Pick's Theorem
Щ…ЩҶ Ш§Ш«ШЁШ§ШӘ ШұЩҲ Ш§ШІ ШұЩҲЫҢ Ш§ЩҲЩҶ ШөЩҒШӯЩҮ Щ…ЫҢ ЩҶЩҲЫҢШіЩ… ШЁШұШ§ШӘЩҲЩҶ:
ЩӮШ¶ЫҢЩҮ ЩҫЫҢЪ©: ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ ЫҢЪ© ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ШіШ§ШҜЩҮ ШұЩҲЫҢ ЫҢЪ© ШҙШЁЪ©ЩҮ Ш§ШІ ЩҶЩӮШ§Ш· ЩҮЩ… ЩҒШ§ШөЩ„ЩҮ (ШҜШіШӘЪҜШ§ЩҮ Щ…Ш®ШӘШөШ§ШӘ ШЁШ§ Щ…Ш®ШӘШөШ§ШӘ ШөШӯЫҢШӯ ) ШҜШ§ШҜЩҮ ШҙШҜЩҮ ШЁШ§ШҙШҜ ШЁЩҮ Ш·ЩҲШұЫҢЪ©ЩҮ ЩҮШұ ШұШ§Ші Ш§ЫҢЩҶ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ШұЩҲЫҢ ЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢЩҶ ЩҶЩӮШ§Ш· ЩӮШұШ§Шұ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ. Ш§ЪҜШұ $i$ ШӘШ№ШҜШ§ШҜ ЩҶЩӮШ§Ш· Ш§ЫҢЩҶ ШҙШЁЪ©ЩҮ Ъ©ЩҮ ШҜШұЩҲЩҶ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ЩҲ $b$ ШӘШ№ШҜШ§ШҜ ЩҶЩӮШ§Ш· Ш§ЫҢЩҶ ШҙШЁЪ©ЩҮ Ъ©ЩҮ ШұЩҲЫҢ Щ…ШұШІ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ( ЫҢШ№ЩҶЫҢ Ш§Ш¶Щ„Ш§Ш№ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ) ЩӮШұШ§Шұ ШҜШ§ШұШҜ ШЁШ§ШҙЩҶШҜ ШўЩҶЪҜШ§ЩҮ Щ…ШіШ§ШӯШӘ Ш§ЫҢЩҶ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ШұШ§ Ъ©ЩҮ ШЁШ§ $A$ ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢ ШҜЩҮЫҢЩ… ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§: $$A=i+\frac b2-1$$
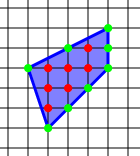
Ш§Ш«ШЁШ§ШӘ: ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ $P$ ЫҢЪ© ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ЩҲ $T$ ЫҢЪ© Щ…Ш«Щ„Ш« ШЁШ§ШҙШҜ Ъ©ЩҮ ШҜШ§ШұШ§ЫҢ ЫҢЪ© Ш¶Щ„Ш№ Щ…ШҙШӘШұЪ© ШЁШ§ШҙЩҶШҜ. ЩҮЩ…ЪҶЩҶЫҢЩҶ ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ ЩӮШ¶ЫҢЩҮ ЩҫЫҢЪ© ШЁШұШ§ЫҢ $p$ЩҲ $T$ ШЁЩҮ ШөЩҲШұШӘ Ш¬ШҜШ§ЪҜШ§ЩҶЩҮ ШЁШұЩӮШұШ§Шұ ШЁШ§ШҙШҜ. ЩҶШҙШ§ЩҶ Щ…ЫҢ ШҜЩҮЫҢЩ… ЩӮШ¶ЫҢЩҮ ЩҫЫҢЪ© ШЁШұШ§ЫҢ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ $PT$ Ъ©ЩҮ Ш§ШІ $P$ ЩҲ $T$ ШӘШҙЪ©ЫҢЩ„ ШҙШҜЩҮ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ.
ЪҶЩҲЩҶ $P$ ЩҲ $T$ ШҜШ§ШұШ§ЫҢ ЫҢЪ© Ш¶Щ„Ш№ Щ…ШҙШӘШұЪ© ЩҮШіШӘЩҶШҜ Щ„Ш°Ш§ ШӘЩ…Ш§Щ… ЩҶЩӮШ§Ш· ШұЩҲЫҢ Ш§ЫҢЩҶ Ш¶Щ„Ш№ Щ…ШҙШӘШұЪ© ШЁЩҮ ЩҶЩӮШ§Ш· ШҜШұЩҲЩҶЫҢ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ Ш¬ШҜЫҢШҜ $PT$ ШӘШЁШҜЫҢЩ„ Щ…ЫҢ ШҙЩҲЩҶШҜШҢ ШЁЩҮ Ш¬ШІ ШЁШұШ§ЫҢ ШҜЩҲ ЩҶЩӮШ·ЩҮ Ш§ЩҶШӘЩҮШ§ЫҢЫҢ Ш§ЫҢЩҶ Ш¶Щ„Ш№ Щ…ШҙШӘШұЪ© Ъ©ЩҮ ЩҶЩӮШ§Ш· ШұЩҲЫҢ Щ…ШұШІ ШЁШ§ЩӮЫҢ Щ…ЫҢ Щ…Ш§ЩҶЩҶШҜ. Ш§ЪҜШұ ШӘШ№ШҜШ§ШҜ ЩҶЩӮШ§Ш· Щ…ШұШІЫҢ ШұЩҲЫҢ Ш¶Щ„Ш№ Щ…ШҙШӘШұЪ© ШұШ§ ШЁШ§ $c$ ЩҶЩ…Ш§ЫҢШҙ ШҜЩҮЫҢЩ… ШҜШ§ШұЫҢЩ…:
$$i_{PT}=i_P+i_T+(c-2)$$
Ш§ШІ Ш·ШұЩҒЫҢ ШЁШұШ§ЫҢ ШӘШ№ШҜШ§ШҜ Ш¶Щ„Ш№ЩҮШ§ ЩҮЩ… ШҜШ§ШұЫҢЩ…:
$$b_{PT}=(b_P+b_T)-2(c-2)-2$$
ШҜШұ ЩҲШ§ЩӮШ№ ЪҶЩҲЩҶ ЩҲЩӮШӘЫҢ ШӘШ№ШҜШ§ШҜ ЩҶЩӮШ§Ш· ШұЩҲЫҢ Ш§Ш¶Щ„Ш§Ш№ $b_P$ ЩҲ $b_T$ ШұШ§ Щ…ЫҢ ШҙЩ…Ш§ШұЫҢЩ… ШҜЩҲ ШЁШ§Шұ ЩҶЩӮШ§Ш·ЫҢ ШұШ§ Ъ©ЩҮ ШҜШұ ЩҮШұ ШҜЩҲ ШҙЪ©Щ„ Щ…ШҙШӘШұЪ© ЩҮШіШӘЩҶШҜ Щ…ЫҢ ШҙЩ…Ш§ШұЫҢЩ… ЩҫШі ШҜШұ ЩҒШұЩ…ЩҲЩ„ ШЁШ§Щ„Ш§ ШҜШұ ШўШ®Шұ $-2(c-2)$ ШұШ§ ЩҶЩҲШҙШӘЫҢЩ… ЩҲ ЪҶЩҲЩҶ ЩҶЩӮШ§Ш· Ш§ЩҶШӘЩҮШ§ЫҢЫҢ Ш¶Щ„Ш№ Щ…ШҙШӘШұЪ© ЩҮЩ… ШҜЩҲ ШЁШ§Шұ ШҙЩ…ШұШҜЩҮ ШҙШҜЩҮ Ш§ЩҶШҜ ШҜШұ ШўШ®Шұ $-2$ ЩҶЩҲШҙШӘЫҢЩ….
ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Ш§ШІ ЩҒШұЩ…ЩҲЩ„ ЩҮШ§ЫҢ ШЁШ§Щ„Ш§ ШҜШ§ШұЫҢЩ… :
$$(i_P+i_T)=i_{PT}-(c-2)\\(b_P+b_T)=b_{PT}+2(c-2)+2$$
Ш§Щ…Ш§ ЩҲШ§Ш¶Шӯ Ш§ШіШӘ Ъ©ЩҮ Щ…ШіШ§ШӯШӘ $PT$ ШЁШ§ Щ…Ш¬Щ…ЩҲШ№ Щ…ШіШ§ШӯШӘ ЩҮШ§ЫҢ $P$ЩҲ $T$ ШЁШұШ§ШЁШұ Ш§ШіШӘ(ЪҶЩҲЩҶ Ш§ЫҢЩҶ ШҜЩҲ ШұШ§ ШЁЩҮ ЩҮЩ… ЪҶШіШЁШ§ЩҶШҜЩҮ Ш§ЫҢЩ… ЩҲ ШҙЪ©Щ„ Ш¬ШҜЫҢШҜ ШұШ§ ШіШ§Ш®ШӘЫҢЩ…) Щ„Ш°Ш§ $A_{PT}=A_P+A_T$
Ш§Щ…Ш§ Щ…Ш§ ЩҒШұШ¶ Ъ©ШұШҜЫҢЩ… Ъ©ЩҮ ЩӮШ¶ЫҢЩҮ ЩҫЫҢЪ© ШЁШұШ§ЫҢ $P$ ЩҲ $T$ ШҜШұШіШӘ ШЁШ§ШҙШҜ Щ„Ш°Ш§ ШҜШ§ШұЫҢЩ…:
$$\begin{align}A_{PT}&=A_P+A_T\\
&=(i_P+\frac{b_P}{2}-1)+(i_T+\frac{b_T}{2}-1)\\
&=(i_P+i_T)+(\frac{b_P+b_T}{2})-2\\
&=(i_{PT}-(c-2))+(\frac{b_{PT}+2(c-2)+2}2)-2\\
&=i_{PT}+\frac{b_{PT}}{2}-1\end{align}$$
ЫҢШ№ЩҶЫҢ Ш«Ш§ШЁШӘ ШҙШҜ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ $PT$ ЩҮЩ… ШҜШұШіШӘ Ш§ШіШӘ.
Щ„Ш°Ш§ Ш§ЪҜШұ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ Ш§ЫҢ Ъ©ЩҮ Ш§ШІ ШЁЩҮ ЩҮЩ… ЪҶШіШЁШ§ЩҶШҜЩҶ $n$ Щ…Ш«Щ„Ш« ШЁЩҮ ЩҲШ¬ЩҲШҜ ШўЩ…ШҜЩҮ ШҜШұШіШӘ ШЁШ§ШҙШҜ ШўЩҶЪҜШ§ЩҮ ШЁШұШ§ЫҢ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ Ш§ЫҢ Ъ©ЩҮ Ш§ШІ ШЁЩҮ ЩҮЩ… ЪҶШіШЁШ§ЩҶШҜЩҶ $(n+1)$ Щ…Ш«Щ„Ш« ШЁЩҮ ЩҲШ¬ЩҲШҜ ШўЩ…ШҜЩҮ Ш§ШіШӘ ЩҶЫҢШІ ЩӮШ¶ЫҢЩҮ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ. Ш§Щ…Ш§ ЩҮЩ…ЩҲШ§ШұЩҮ ЫҢЪ© ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ШұШ§ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ ЪҶЩҶШҜ Щ…Ш«Щ„Ш« ШӘЩӮШіЫҢЩ… Ъ©ШұШҜ. ЩҫШі ШЁШұШ§ЫҢ Ш§Ш«ШЁШ§ШӘ ЩӮШ¶ЫҢЩҮ ШЁЩҮ ЩҲШіЫҢЩ„ЩҮ ЫҢ Ш§ШіШӘЩӮШұШ§ Ъ©Ш§ЩҒЫҢ Ш§ШіШӘ Щ…Ш§ ЩҶШҙШ§ЩҶ ШҜЩҮЫҢЩ… Ъ©ЩҮ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ ЫҢЪ© Щ…Ш«Щ„Ш« ЩҮЩ… ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ. Ш§Щ…Ш§ ШЁШұШ§ЫҢ Ш§Ш«ШЁШ§ШӘ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ Щ…Ш«Щ„Ш« Щ…ШұШ§ШӯЩ„ ШІЫҢШұ ШұШ§ ШЁШ§ЫҢШҜ Ш·ЫҢ Ъ©ШұШҜ:
- ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ ЩҮШұ Щ…ШұШЁШ№ ЩҲШ§ШӯШҜ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ(ЩҮШұ ШұШ§Ші ШҜШ§ШұШ§ЫҢ Щ…Ш®ШӘШөШ§ШӘ ШөШӯЫҢШӯ ШЁШ§ШҙШҜ)
- Ш§ШІ Ш§ЫҢЩҶ ЩҶШӘЫҢШ¬ЩҮ ШЁЪҜЫҢШұЫҢШҜ Ъ©ЩҮ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ ЩҮШұ Щ…ШіШӘШ·ЫҢЩ„ЫҢ Ъ©ЩҮ Ш§Ш¶Щ„Ш§Ш№Шҙ Щ…ЩҲШ§ШІЫҢ Щ…ШӯЩҲШұЩҮШ§ ШЁШ§ШҙЩҶШҜ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ
- Ш§ШІ Ш§ЫҢЩҶ ЩҮЩ… ЩҶШӘЫҢШ¬ЩҮ ШЁЪҜЫҢШұЫҢШҜ Ъ©ЩҮ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ Щ…Ш«Щ„Ш« ЩҮШ§ЫҢ ЩӮШ§ЫҢЩ… Ш§Щ„ШІШ§ЩҲЫҢЩҮ Ъ©ЩҮ Ш§ШІ ЩҶШөЩҒ Ъ©ШұШҜЩҶ Щ…ШіШӘШ·ЫҢЩ„ ШҜШұ ШұШ§ШіШӘШ§ЫҢ ЩӮШ·Шұ ШўЩҶ ШЁЩҮ ЩҲШ¬ЩҲШҜ Щ…ЫҢ ШўЫҢШҜ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ
- ШӯШ§Щ„ ШЁШұШ§ЫҢ ЩҮШұ Щ…Ш«Щ„Ш«ЫҢ ЪҶЩҲЩҶ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁШ§ Ш§Ш¶Ш§ЩҒЩҮ Ъ©ШұШҜЩҶ Щ…Ш«Щ„Ш« ЩҮШ§ЫҢ ЩӮШ§ЫҢЩ… Ш§Щ„ШІШ§ЩҲЫҢЩҮ ШўЩҶ ШұШ§ ШЁЩҮ Щ…ШіШӘШ·ЫҢЩ„ ШӘШЁШҜЫҢЩ„ Ъ©ШұШҜ ЩҲ ЪҶЩҲЩҶ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ Щ…ШіШӘШ·ЫҢЩ„ ЩҮШ§ ЩҲ Щ…Ш«Щ„Ш« ЩҮШ§ЫҢ ЩӮШ§ЫҢЩ… Ш§Щ„ШІШ§ЩҲЫҢЩҮ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ Щ„Ш°Ш§ ШЁШұШ§ЫҢ Щ…Ш«Щ„Ш« Ш§ЩҲЩ„ЫҢЩҮ ЩҮЩ… ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ.
Щ…ШұШӯЩ„ЩҮ ШўШ®Шұ Ш§ШІ Ш§ЫҢЩҶ ШӯЩӮЫҢЩӮШӘ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЫҢЪ©ЩҶШҜ Ъ©ЩҮ Ш§ЪҜШұ ЩӮШ¶ЫҢЩҮ ШЁШұШ§ЫҢ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ $PT$ ЩҲ Щ…Ш«Щ„Ш« $T$ ШҜШұШіШӘ ШЁШ§ШҙШҜ ШўЩҶЪҜШ§ЩҮ ШЁШұШ§ЫҢ $P$ ЩҮЩ… ШҜШұШіШӘ Ш§ШіШӘ. Ъ©ЩҮ Ш§Ш«ШЁШ§ШӘ Ш§ЫҢЩҶ Щ…Ш·Щ„ШЁ ЩҮЩ… Ш®ЫҢЩ„ЫҢ ШҙШЁЫҢЩҮ Ш§Ш«ШЁШ§ШӘЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШЁШ§Щ„Ш§ Ш§ШұШ§ЫҢЩҮ ШҙШҜ.