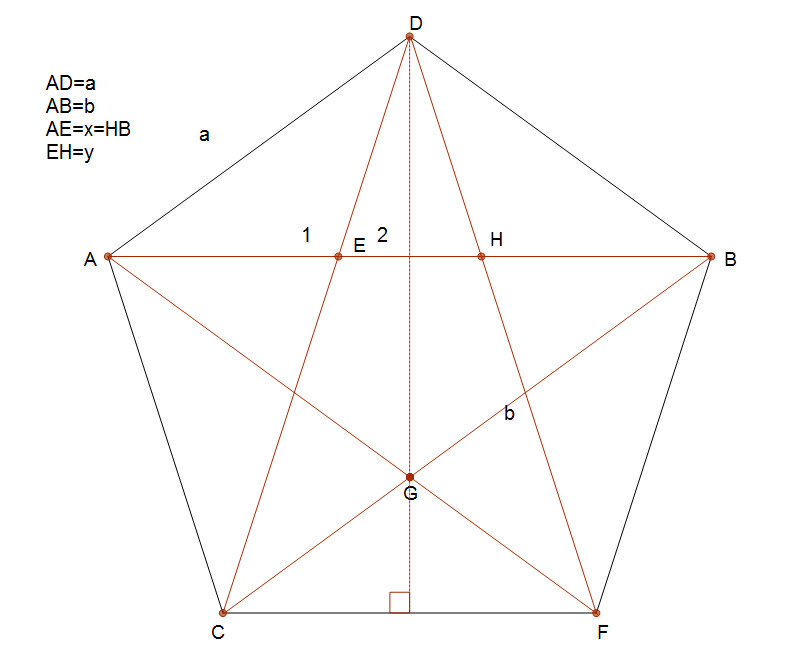
< } math> $$cosC=\frac{CF/2}{CD}=\frac{a}{2b }
\\cosE_1=cos( {\pi}-E_2)=-cos(E_2)=-\frac{a}{2b}$$
$$cosE_2=cosC
\\a^2=x^2+x^2-2x^2cosE_1=x^2(2-2cosE_1)=x^2(2+2cosE_2)
\\a^2=x^2(2+\frac{a}{b}) \rightarrow x=\sqrt{\frac{a^2}{2+\frac{a}{b}}}=\sqrt{\frac{ba^2}{2+a}}$$
$$y+2x=b \rightarrow y=b-2x = b-2 \sqrt{\frac{ba^2}{2+a}}$$