اگر بدون تکرار مدنظر داشته باشیم تعداد کل اعداد چهاررقمی با رقم های 1 و 3 و 5 و 7 و 9 عبارتند از:
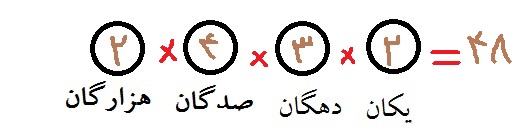
که برای هزارگان فقط دو انتخاب 1 و 3 را ابتدا انتخاب میکنیم سپس برای بقیه جایگاه ها به ترتیب 4 و 3 و 2 انتخاب خواهیم داشت.
حال برای اینکه از بین این 48 عدد تعداد اعداد بخش پذیر بر 5 را انتخاب کنیم(عددی بر 5 بخشپذیر است که رقم یکان آن صفر یا 5 باشد) پس برای یکان تنها یک انتخاب و ان هم 5 را داریم پس میتوان نوشت تعداد اعداد 4رقمی با اعداد 1 و 3 و 5 و 7 و 9 بدون تکرار و کمتر از 5000 برابر است با:
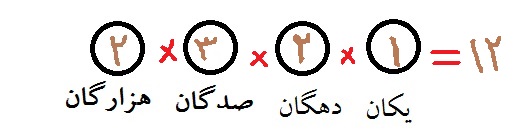
پس طبق تعریف احتمال، احتمال سوال داده شده برابر است با: $ \frac{12}{48}= \frac{1}{4} $ .