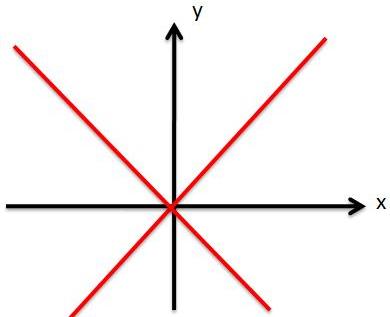
نمودار یک تابع مجموعه تمام زوج های مرتب $(x,f(x)) $ است. برای توابع پیوسته میتوان شکل تابع را در دستگاه مختصات به راحتی رسم کرد و آن را منحنی می نامیم اما برای بعضی از توابع نا پیوسته مانند مثال گفته شده این کار بطور دقیق امکان پذیر نیست. آن هم به این خاطر است که بین هر دو عدد گویا یک عدد گنگ وجود دارد و برعکس و این مجموعه ها چگال هستند.
بعضی از افراد به طور تقریبی نمودار تابع ذکر شده را به صورت زیر رسم میکنن ولی در کنار آن این نکته ضروری را هم ذکر میکنند که در هر نقطه روی محور یکی از نمودارها دارای حفره است و دیگری توپر است.
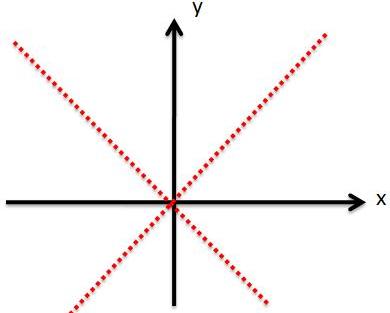
یا حتی به صورت زیر هم چنین توابعی رو رسم میکنند(بسته به سلیقه نویسنده داره و حتما کنار شکل توضیحات لازم گفته می شود.)