نقطه ای در صفحه بیابید که از ان نقطه دو خط مماس برسهمی y=x² بتوان رسم کرد و این خط ها برهم عمود باشند.این مسئله چند جواب دارد؟

Question

نقطه‌ای در صفحه بیابید که از آن نقطه دو خط مماس برسهمی $y=x^2$ بتوان رسم کرد و این خط‌ها برهم عمود باشند. این مسأله چند جو‌اب دارد؟

تلاش من: این مسأله را به روشی طولانی حل کردم خودم و جواب $-\frac{1}{4}$ را بدست آوردم. اما بسیار طولانی است و ظاهرا روش اصولی‌تری نیز هست، به همین دلیل قصد داشتم ببینم بقیه به چه شکل این مسأله را حل می‌کنند. من ابتدا معادله خط مماس تابع در حالت کلی را نوشتم سپس حالتی که در آن شیب، قرینه و معکوس هست در نظر گرفتم و دوباره معادله جدید بر آن اساس نوشتم و حل کردم اما طولانی شد.

Comments

@Navid_yar به سال کتاب مورد نظر اشاره کنید. چون فقط یک نظام قدیم و جدید مطلق نداریم. کتاب‌های آموزش و پرورش و سیستم مدرسه‌ها به دفعات تغییر کرده‌اند بنابراین یک نظام قدیم نداریم بلکه نظام‌های قدیم داریم.

Answer 1

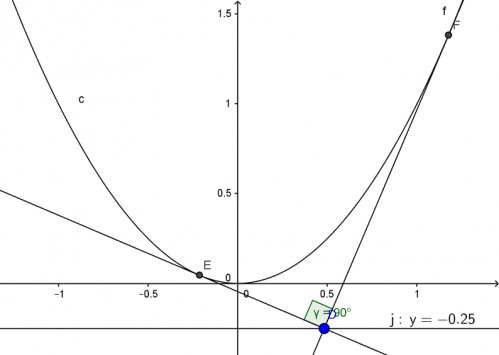
اگر نقطه را $\big( x_{0}, y_{0} \big)$ فرض کنم و معادله خطوط را با شیب $m$ رابنویسیم و آن را با سهمی قطع دهیم یعنی :

$\begin{cases}y=mx-mx_{0}+y_{0} & \\y=x^2 & \end{cases}$

درنتیجه :

$x^2-mx+mx_{0}-y_{0}=0$

اکنون وقتی برای مماس شدن تماس این خطوط با سهمی باید فقط در یک $x$ رخ بدهد پس $\triangle =0$

$m^2-4mx_{0}+4y_{0}=0$

اما از آنجاییکه $m$ های این معادله حاصلضربشان به دلیل عمود بودن دو خط مماس باید $-1$ گردد پس:

$$\frac{c}{a}=-1 \Rightarrow 4y_{0}=-1 \Rightarrow \color{red}{y_{0}= -\frac{1}{4}}$$

یعنی از تمام نقاط روی خط ثابت$y= -\frac{1}{4}$ می توان این کار را انجام داد.

Comments

@Navid_yar راه شما همین بود؟