ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ $dx$ ШЁЩҮ Щ…Ш№ЩҶШ§ЫҢ $\Delta x$ Ш§ШіШӘ ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ $\Delta x\to 0$ ЩҲ $\Delta x$ ШЁШұШ§ШЁШұ ШЁШ§ $|x_2-x_1|$ Ш§ШіШӘ. ШӘШ№ШұЫҢЩҒ Ш§ЩҶШӘЪҜШұШ§Щ„ ШЁШ§ Ъ©Щ…Ъ© ШӯШҜ Ш¬Щ…Ш№ ШұЫҢЩ…Ш§ЩҶ ШЁШұШ§ЫҢ Щ…ШіШ§ШӯШӘ ШІЫҢШұ ЩҶЩ…ЩҲШҜШ§Шұ ШұШ§ ШЁЩҮ ЫҢШ§ШҜ ШўЩҲШұЫҢШҜ. $\Delta x$ ЩҫЩҮЩҶШ§ (Ш№ШұШ¶) Щ…ШіШӘШ·ЫҢЩ„вҖҢЩҮШ§ ШЁЩҲШҜ. ЪҶЩҲЩҶ $\Delta x$ ЩҶШ§Щ…ЩҶЩҒЫҢ Ш§ШіШӘ ЩҫШі $dx$ ЩҶЫҢШІ ЩҶШ§Щ…ЩҶЩҒЫҢ Ш§ШіШӘ.ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ЩҶЩҲШҙШӘЩҶЩҗ $dx$ ЫҢШ§ $|dx|$ ШӘЩҒШ§ЩҲШӘЫҢ ШЁШұШ§ЫҢШӘШ§ЩҶ Ш§ЫҢШ¬Ш§ШҜ ЩҶШ®ЩҲШ§ЩҮШҜ Ъ©ШұШҜ. ЪҶЫҢШІЫҢ Ъ©ЩҮ Щ…ШҜЩҶШёШұШӘШ§ЩҶ Ш§ШіШӘ $\int|f(x)|dx$ Ш§ШіШӘ. ЩҲ Ш§Щ…Ш§ ШӯШҜШіЫҢ Ъ©ЩҮ ШІШҜЫҢШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Ш§Ш«ШЁШ§ШӘвҖҢЩҮШ§ ШЁШ§ЫҢШҜ ЩҫЫҢЩҲШіШӘЩҮ ШЁШ§ШҙЩҶШҜШҢ ЩҮШұ ЪҜШ§ЩҮ Ш§ШіШӘШҜЩ„Ш§Щ„ЫҢ Ъ©ШұШҜЫҢШҜ Ъ©ЩҮ ШЁЫҢЩҶ Ш¬Щ…Щ„ЩҮвҖҢЩҮШ§ЫҢШӘШ§ЩҶ ЩҫШұШҙ ЫҢШ§ Ш№ШҜЩ… ЩҲШ¬ЩҲШҜ Ш№Щ„ШӘ ШӯШі Щ…ЫҢвҖҢШҙЩҲШҜШҢ ШЁШ§ЫҢШҜ ШЁЩҮ ШҜШұШіШӘЫҢ ШўЩҶ ШҙЪ© Ъ©ЩҶЫҢШҜ. ЪҜЩҒШӘЩҮвҖҢШ§ЫҢШҜ Ъ©ЩҮ В«ЩҮЫҢЪҶ ШӘШ§ШЁШ№ЫҢ ЩҶЩ…ЫҢЩҶЩҲШ§ЩҶШҜ ШЁЩҮ ШҙЪ©Щ„ ЫҢЪ© Ш№ШЁШ§ШұШӘ ЩӮШҜШұ Щ…Ш·Щ„ЩӮЫҢ ШЁШ§ШҙШҜШӣ Щ…ЪҜШұ Ш§ЫҢЩҶЪ©ЩҮ ШҜЫҢЩҒШұШ§ЩҶШіЩ„ ШўЩҶ ШӘШ§ШЁШ№ ШЁШұШ§ШЁШұ ШөЩҒШұ ШЁШ§ШҙШҜВ». ЫҢШ№ЩҶЫҢ Ш§ЪҜШұ ЩҒШұШ¶ Ъ©ЩҶЫҢЩ… Щ…ШҙШӘЩӮ ШӘШ§ШЁШ№ЫҢ ШЁЩҮ ШҙЪ©Щ„ ЩҒШұЩ…ЩҲЩ„ЫҢ ЩӮШҜШұЩ…Ш·Щ„ЩӮвҖҢШҜШ§Шұ ЩҶЩҲШҙШӘЩҮ ШҙЩҲШҜШҢ ШўЩҶЪҜШ§ЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢЩ… ЩҶШӘЫҢШ¬ЩҮ ШЁЪҜЫҢШұЫҢЩ… Ъ©ЩҮ Ш§ЫҢЩҶ Щ…ШҙШӘЩӮ ШөЩҒШұ Ш§ШіШӘ! Ш®ШЁ ШўЫҢШ§ ЪҶЩҶЫҢЩҶ ЩӮШ¶ЫҢЩҮвҖҢШ§ЫҢ ШұШ§ Ш¬Ш§ЫҢЫҢ ШҜЫҢШҜЩҮвҖҢШ§ЫҢШҜШҹ Ш§ЪҜШұ ШЁЩ„ЫҢ Ш§ШіШӘЩҶШ§ШҜ Ъ©ЩҶЫҢШҜШҢ Ш§ЪҜШұ Ш®ЫҢШұШҢ ЩҫШі ЫҢШ№ЩҶЫҢ Ш§ШҜШ№Ш§ЫҢ Ш®ЩҲШҜШӘШ§ЩҶ Ш§ШіШӘ. Ш§Ъ©ЩҶЩҲЩҶ Ъ©ЩҮ Ш§ШҜШ№Ш§ЫҢ Ш®ЩҲШҜШӘШ§ЩҶ Ш§ШіШӘШҢ Ш№Щ„ШӘ ШўЩҶ ЪҶЫҢШіШӘШҹ ЩӮШҜШұЩ…Ш·Щ„ЩӮ ШЁЩҮ ШӘЩҶЩҮШ§ЫҢЫҢ ШЁЩҮ Щ…Ш№ЩҶШ§ЫҢ ШөЩҒШұ ШЁЩҲШҜЩҶ ЩҶЫҢШіШӘ. ЩҫШі Ш§ЫҢЩҶШ¬Ш§ ЫҢЪ© Ш®Щ„Ш§ШЎ ЩҮШіШӘ. ЩҫШі ЪҶЫҢШІЫҢ Ъ©ЩҮ ЩҶЩҲШҙШӘЩҮвҖҢШ§ЫҢШҜ ЫҢЪ© Ш§Ш«ШЁШ§ШӘ ЩҶЫҢШіШӘ. Ш§Щ…Ш§ ШўЫҢШ§ ШҜШұШіШӘ Ш§ШіШӘШҹ Ш®ЫҢШұ. Щ…Ш«Ш§Щ„ ЩҶЩӮШ¶ Ш®ЫҢЩ„ЫҢ ШіШ§ШҜЩҮ. ЩӮШұШ§Шұ ШҜЩҮЫҢШҜ $f(x)=e^x$. Щ…ШҙШӘЩӮ ШўЩҶ ЪҶЩҮ Щ…ЫҢвҖҢШҙЩҲШҜШҹ Ш®ЩҲШҜШҙ Щ…ЫҢвҖҢШҙЩҲШҜ $f'(x)=e^x$. ЩҲ ЪҶЩҲЩҶ ШЁЩҸШұШҜ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ Щ…Ш«ШЁШӘ Ш§ШіШӘ ЩҫШі ЪҜШ°Ш§ШҙШӘЩҶ ЫҢШ§ ЩҶЪҜШ°Ш§ШҙШӘЩҶ ЩӮШҜШұЩ…Ш·Щ„ЩӮ ШӘЩҒШ§ЩҲШӘЫҢ Ш§ЫҢШ¬Ш§ШҜ ЩҶШ®ЩҲШ§ЩҮШҜЪ©ШұШҜ ЩҫШі Ш§ЪҜШұ ШЁЩҶЩҲЫҢШіЩ… $f'(x)=|e^x|$ ЪҶЫҢШІ ЩҶШ§ШҜШұШіШӘЫҢ ЩҶЩҶЩҲШҙШӘЩҮвҖҢШ§Щ…. Ш§Щ…Ш§ ШўЫҢШ§ Ш§ШҜШ№Ш§ЫҢ ШҙЩ…Ш§ Ъ©ЩҮ ЪҶЩҲЩҶ Щ…ШҙШӘЩӮ ЩӮШҜШұЩ…Ш·Щ„ЩӮвҖҢШҜШ§Шұ ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮвҖҢШ§ШіШӘ ЩҫШі Щ…ШҙШӘЩӮ ШөЩҒШұ Ш§ШіШӘШҢ ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ШөШ§ШҜЩӮ Ш§ШіШӘШҹ Ш®ЫҢШұ. ЩҫШі Ш§ЫҢЩҶ ЫҢЪ© Щ…Ш«Ш§Щ„ ЩҶЩӮШ¶ ШЁШұШ§ЫҢ ШӯШҜШі ШҙЩ…Ш§ШіШӘ.
ЩҲ Ш§Щ…Ш§ ЪҶЪҜЩҲЩҶЩҮ Ш§ЩҶШӘЪҜШұШ§Щ„ ЫҢЪ© Ш№ШЁШ§ШұШӘ ЩӮШҜШұЩ…Ш·Щ„ЩӮвҖҢШҜШ§Шұ ШұШ§ Щ…ШӯШ§ШіШЁЩҮ Ъ©ЩҶЫҢЩ…. Щ…Ш«Ш§Щ„ ШіШ§ШҜЩҮ Ъ©ЩҮ ШўЩӮШ§ЫҢ @mahdiahmadileedari ШЁШ§ ЩҒШұШ¶ Щ…Ш№ЫҢЩҶ ШЁЩҲШҜЩҶ Ш§ЩҶШӘЪҜШұШ§Щ„ ЩҶЩҲШҙШӘЩҶШҜ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ. ШҜШұ ЩҲШ§ЩӮШ№ Ш§ЫҢШҙШ§ЩҶ ШҜШұ ЩҫШ§ШіШ®ШҙШ§ЩҶ ЩҒШұШ¶ Ъ©ШұШҜЩҮвҖҢШ§ЩҶШҜ Ъ©ШұШ§ЩҶвҖҢЩҮШ§ЫҢ Ш§ЫҢЩҶ Ш§ЩҶШӘЪҜШұШ§Щ„ Щ…ЩҶЩҒЫҢ ЫҢЪ© ЩҲ ЫҢЪ© ЩҮШіШӘЩҶШҜ ЩҲЩ„ЫҢ ШҜШұ ЩҶЩҲШҙШӘЩҶ ЩҒШұЩ…ЩҲЩ„вҖҢЩҮШ§ Ш§ЫҢЩҶ Ъ©ШұШ§ЩҶвҖҢЩҮШ§ ШұШ§ Ш¬Ш§ Ш§ЩҶШҜШ§Ш®ШӘЩҮвҖҢШ§ЩҶШҜ. Ш§Щ…Ш§ ШӯШӘЫҢ ШЁШұШ§ЫҢ ШӯШ§Щ„ШӘ ЩҶШ§Щ…Ш№ЫҢЩҶ ЩҮЩ… Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Щ…ШӯШ§ШіШЁЩҮ ШұШ§ Ш§ЩҶШ¬Ш§Щ… ШҜШ§ШҜ.
$$\begin{align}
\int |x|dx &= \begin{cases}
\int xdx & ;\;x\geq 0\\
\int -xdx & ;\; x<0
\end{cases}\\
&= \begin{cases}
\frac{1}{2}x^2 & ;\;x\geq 0\\
-\frac{1}{2}x^2 & ;\; x<0
\end{cases}
\end{align}$$
ШӯШӘЫҢ ШЁЩҮШӘШұШҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш§ШІ ШӘШ§ШЁШ№ Ш№Щ„Ш§Щ…ШӘ ЫҢШ№ЩҶЫҢ $\rm{sgn}(x)$ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ШұШҜ Ъ©ЩҮ ЩҮШұ Ш№ШҜШҜ ШӯЩӮЫҢЩӮЫҢ ШұШ§ ШЁЩҮ Ш№Щ„Ш§Щ…ШӘШҙ Щ…ЫҢвҖҢШЁШұШҜ ЫҢШ№ЩҶЫҢ Ш№ШҜШҜЩҮШ§ЫҢ Щ…Ш«ШЁШӘ ШұШ§ ШЁЩҮ ЫҢЪ©ШҢ Ш№ШҜШҜЩҮШ§ЫҢ Щ…ЩҶЩҒЫҢ ШұШ§ ШЁЩҮ Щ…ЩҶЩҒЫҢ ЫҢЪ© ЩҲ ШөЩҒШұ ШұШ§ ШЁЩҮ ШөЩҒШұ Щ…ЫҢвҖҢЩҶЪҜШ§ШұШҜ.
$$\int |x|dx=\rm{sgn}(x)\frac{x^2}{2}+c$$
Ъ©ЩҮ $c$ ЩҶЫҢШІ ШҜШұ ШўШ®Шұ ЫҢЪ© Ш№ШҜШҜ Ш«Ш§ШЁШӘ Ш§ШіШӘ.
ШЁШұШ®ЫҢ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§ШұЩҮШ§ЫҢ ШұЫҢШ§Ш¶ЫҢ ЩҶЫҢШІ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШұШ§ Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢвҖҢШҜЩҮЩҶШҜ Щ…Ш§ЩҶЩҶШҜ Щ…ЫҢЩҫЩ„ Maple ЩҲЩ„ЫҢ ЩҶЩҮ ЩҮШұ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§ШұЫҢШҢ ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ ШЁШіШӘЩҮЩ” Sympy ШЁШұШ§ЫҢ ШІШЁШ§ЩҶ ШЁШұЩҶШ§Щ…ЩҮвҖҢЩҶЩҲЫҢШіЫҢЩҗ Python ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ Ш§ЫҢЩҶ Ш§ЩҶШӘЪҜШұШ§Щ„ ШұШ§ ШЁЪҜЫҢШұШҜ.
ШҜШұ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ Щ…ЫҢЩҫЩ„:
int( abs( x ), x );
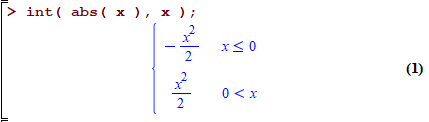
ШЁШіШӘЩҮЩ” Sympy ШІШЁШ§ЩҶ ШЁШұЩҶШ§Щ…ЩҮвҖҢЩҶЩҲЫҢШіЫҢ ЩҫШ§ЫҢШӘЩҲЩҶ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ $\int xdx$ ШұШ§ Щ…ШӯШ§ШіШЁЩҮ Ъ©ЩҶШҜ ЩҲЩ„ЫҢ $\int |x|dx$ ШұШ§ ШЁЩҮ ЩҮЩ…Ш§ЩҶ ШҙЪ©Щ„ ШЁШұШ§ЫҢШӘШ§ЩҶ ШЁШұЩ…ЫҢвҖҢЪҜШұШҜШ§ЩҶШҜ.
from sympy import *
x = Symbol( 'x' )
integrate( x, x )
integrate( abs( x ), x )
init_printing( use_unicode = False, wrap_line = False )
integrate( x, x )
integrate( abs( x ), x )
ШҜШұ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ Щ…ШӘЩ„ШЁ:
syms x
int( abs( x ), x )
ЩҮЩ…Ш§ЩҶ ЪҜЩҲЩҶЩҮ Ъ©ЩҮ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢШҜШҢ Ш®ШұЩҲШ¬ЫҢЩҗ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§ШұЩҗ Щ…ШӘЩ„ШЁ Matlab Ш§ШІ ШӘШ§ШЁШ№Щҗ Ш№Щ„Ш§Щ…ШӘ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ШұШҜЩҮвҖҢШ§ШіШӘ Ъ©ЩҮ ШЁЩҮ Ш¬Ш§ЫҢ Ъ©ЩҲШӘШ§ЩҮвҖҢШҙШҜЩҮЩ” $\rm{sgn}$ Ш§ШІ ЩҲШ§ЪҳЩҮЩ” Ъ©Ш§Щ…Щ„ $\rm{sign}$ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ШұШҜЩҮвҖҢШ§ШіШӘ.