روش اول :
اگر در رسم نمودار تبحر دارید برای سوالات تستی مخصوصا رسم نمودار میتونه خیلی کمک کنه. ابتدا نمودار را رسم می کنیم و روی هر نقطه صحیح یک خط موازی محور $ x $ ها رسم میکنیم و قسمتی از نمودار را که بین دو خط قرار دارد بر خط پایینی تصویر می کنیم برای این سوال داریم:
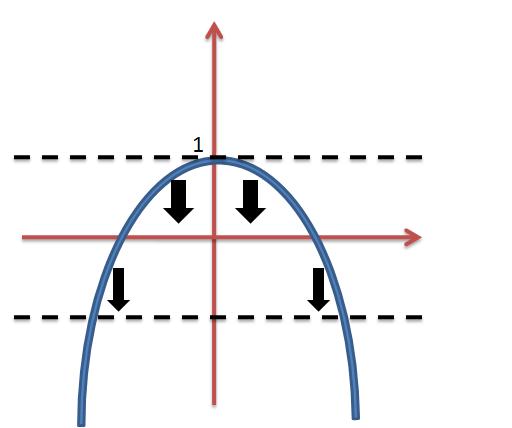
در نتیجه به شکل زیر می رسیم:
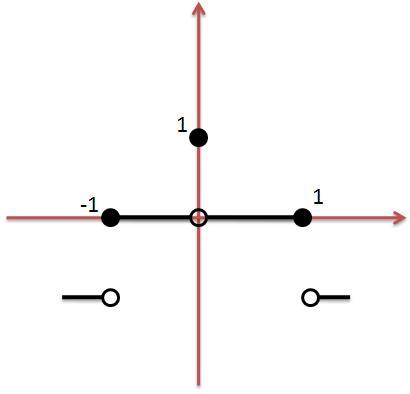
که با توجه به شکل در نقطه $x=0$ مقدار تابع $1$ اما حد صفر است لذا پیوسته نیست اما در بقیه نقاط در بازه $[-1,1]$ پیوسته است. در نقطه $x=-1$
از راست تابع تعریف می شود که در این نقطه مقدار تابع با حد هردو برابر $0$ هستند و در $x=1$به طور مشابه است.
روش دوم:
تابع جز صحیح معمولا در نقاطی که داخل جز صحیح ، صحیح باشد پیوسته نیست و در بقیه نقاط پیوسته است پس با پیدا کردن نقاطی که داخل جز صحیح، صحیح می شود نقاط محتمل برای ناپیوستگی را بدست می آوریم و کافیه پیوستگی در آن نقاط را بررسی کنیم.
اولا
$$-1 \leq x \leq 1 \Rightarrow 0 \leq x^{2} \leq 1 \Rightarrow -1 \leq -x^{2} \leq 0 \Rightarrow 0 \leq 1-x^{2} \leq 1$$
پس فقط دو حالت داریم:
1) $ 1-x^{2} =1 \Rightarrow x^{2}=0 \Rightarrow x=0 $ که با بررسی این نقطه مقدار تابع $1$ اما حد صفر است لذا پیوسته نیست
2)$ 1-x^{2} =0 \Rightarrow x^{2}=1 \Rightarrow x= \overline{+} 1 $ که این نقاط نقاط انتهایی هستند . به راحتی دیده می شود که تابع پیوسته است.
اگر باز سوالی داشتید در یک دیدگاه بفرمایید .