ابتدا ارتفاع مثلث( که نیمساز و میانه نیز است) را رسم میکنیم سپس $ MC$ را امتداد می دهیم تا ارتفاع را در $N $ قطع کند سپس $ N $ را به $ B $ وصل می کنیم تا شکل زیر بدست آید.
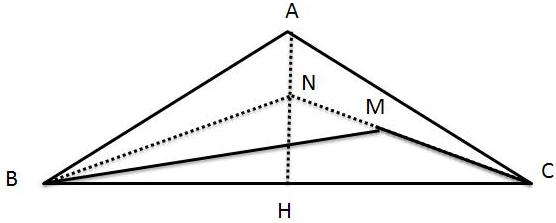
حال از اینکه $ N $ روی عمود منصف ضلع $BC $ قرار دارد داریم:
$$ \widehat{NBC}= \widehat{NCB} =30 $$
پس از اینکه طبق فرض $ \widehat{MBC}=10 $ داریم که $ \widehat{NBM} =20 $
از اینکه $ AH$ نیمساز نیز است داریم $ \widehat{BAN}=40 $
همچنین $ \widehat{ABN} = \widehat{ABH} - \widehat{NBH} =50-30=20 $
از اینکه $ \widehat{BMN} $ زاویه خارجی مثلث $BMC $ است پس برابر مجموع دو زاویه داخلی غیر مجاور یعنی $ \widehat{MBC} $ و $ \widehat{MCB} $ است پس برابر است با $40 $
پس دو مثلث $ ABN $ و $ BNM $ به حالت دوزاویه و ضلع بین همنهشت هستند لذا اضلاع نظیر یعنی $ AB $ و $ BM $ برابر هستند و حکم ثابت شد.