کافیه خطی موازی قاعده که از نقطه $ $ می گذرد را رسم کنیم و 4 بار فیثاغورس را بکار ببریم.(از اینکه عبارت ها توان دوم هستند و با مستطیل سروکار داریم حدس زده شد) برای راحتی نامگذاری های زیر را انجام می دهیم.
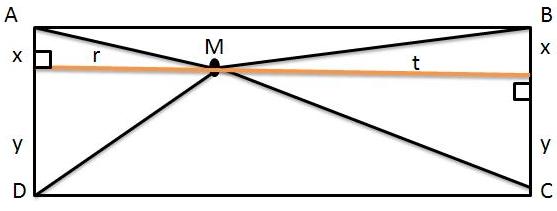
$$ \begin{cases} AM^{2}= x^{2} + r^{2} \\DM^{2}= y^{2} + r^{2}\\BM^{2}= x^{2} + t^{2}\\CM^{2}= y^{2} + t^{2}\end{cases} $$
حال سوال گفته $AM^{2}+CM^{2} $ که با جایگذاری داریم:
$$AM^{2}+CM^{2}= x^{2} + r^{2}+y^{2} + t^{2} $$
به طور مشابه
$$BM^{2}+DM^{2}= x^{2} + r^{2}+y^{2} + t^{2} $$
لذا برابرند.