Question

در مثلث Abc طول میانه های ma=15 و mb=۹ و a=14. مساحت این مثلث چقدر است؟د‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌

Comments

منظورشون از ma میانه وارد بر ضلع a  و همچنین منظور از mb میانه وارد بر ضلع b  می باشد

---

@mahdiahmadileedari
لطفا لینک سوال حل شده رو درج بفرمایید. من هر چی گشتم سوال اصلی رو پیدا نکردم

Answer 1

سلام طبق قضیه میانه ها در مثلث $ABC$ داریم: $$ 2 m_{a} ^{2} =b^{2} + c^{2} - \frac{ a^{2} }{2} $$ $$ 2 m_{b} ^{2} =a^{2} + c^{2} - \frac{ b^{2} }{2} $$ با کم کردن ۲ مورد فوق داریم $$2(m_a^2-m_b^2)= b^2-a^2 - \frac{ a^{2} }{2} + \frac{ b^{2} }{2}= \frac{3}{2} (b^2-a^2) $$ با معلوم بودن میانه وارد بر a و b و نیز طول ضلع a، مقدار b قابل محاسبه خواهد بود. حال مقدار c نیز از یکی از دو روابط میانه که ابتدا نوشتم قابل محاسبه خواهد بود. با معلوم بودن ۳ ضلع مساحت از طریق دستور هرون قابل محاسبه خواهد بود. محاسبات به عهده خودتان.

سلام راهی که بیان شد دارای محاسبات طولانی است. راه دیگه ای رو در ادامه می نویسم.

با توجه به این که میانه ها به نسبت 1 به 2 یکدیگر را قطع میکنند لذا $$AO=10,OM=5,BO=6,OM'=3$$ و در مثلث BOM طبق قضیه کسینوس ها داریم: $$7^2=5^2+6^2-2 \times 5 \times 6 \times cos( \alpha ) \rightarrow sin( \alpha )= \frac{1}{5} \rightarrow sin( \alpha )= \sqrt{1- (\frac{1}{5})^2 }= \frac{2 \sqrt{6} }{5} $$ پس مساحت $AOM'$ برابر است با: $$ \frac{1}{2}AO.OMsin(\alpha) =\frac{1}{2} \times 10 \times 3 \times\frac{2 \sqrt{6} }{5}=6 \sqrt{6} $$ می دانیم 3 میانه مثلث را به 6 مثلث هم مساحت تقسیم میکنند. لذا مساحت کل 6 برابر این مقدار یعنی $36 \sqrt{6} $ است.

سلام

Answer 2

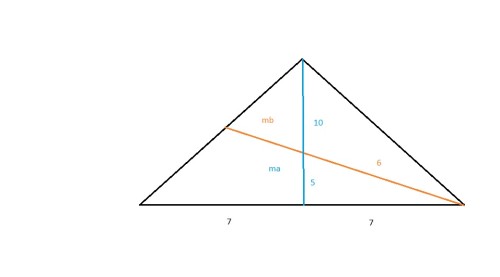
برای حل این سوال باید به دو نکته توجه کرد:

_میانه ها یکدیگر را به نسبت 2 به 1 تقسیم می کنند

_میانه ها مثلث را به 6 مثلث هم مساحت تقسیم می کنند

با توجه به این دو نکته و تصویر درج شده واضح است که اضلاع مثلث گوشه پایینی قابل محاسبه است. حالا با استفاده از دستور هرون مساحت مثلث کوچک را بدست میاوریم:

$$ S = \sqrt{p(p-a)(p-b)(p-c)} $$ p = نصف محیط مثلث

a,b,c = اضلاع مثلث

$$ P = \frac{6 + 5 + 7}{2} = 9 $$ $$S = \sqrt{9(9-6)(9-5)(9-7)} = 6 \sqrt{6} $$

در نتیجه مساحت مثلث اصلی 6 برابر اندازه مساحت مثلث کوچکتر بدست آمده است: $$36 \sqrt{6} $$