ابتدا خط $ QA $ را موازی خط $ d $(یا عمود بر $ DH $) رسم می کنیم
به سادگی دیده می شود که چهار ضلعی $ AQHM$ مستطیل است لذا $ AM=QH $
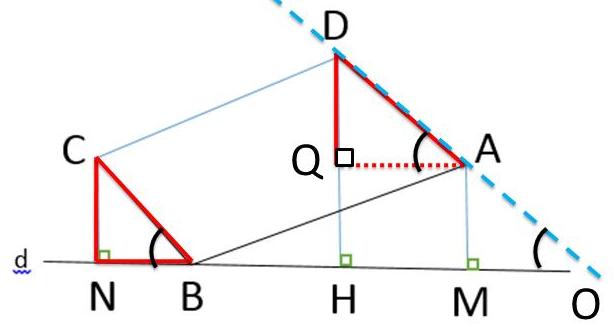
حال دو مثلث مشخص شده در شکل به حالت وتر و یک زاویه همنهشت هستند. لذا $ NC=QD $ حال دو رابطه ی بدست آمده را مقایسه کنیم داریم:
$$ CN+AM=QD+QH=DH$$
از آنجایی که چهار ضلعی $ AQHM$ مستطیل است لذا $ QA$ با
$ HM=d $ موازی است و خط مورب $ AD $ این دو را قطع کرده است. پس زاویه ی $ A $ با زاویه ی $O$ برابر است.
از طرف دیگر $ BC $ با $ AD $ موازی است(اضلاع متوازی الاضلاع) و خط مورب $ d $ این دو راقطع کرده لذا زاویه ی $O$ با $ B $ برابر است.
و این حکم را ثابت می کند.