با توجه به اینکه $ AD $ نیمساز است لذا $ \widehat{CAD} = \widehat{BAD} $ حال اگر نشان دهیم $ \widehat{CAH} = \widehat{BAM} $ آنگاه حکم ثابت می شود.
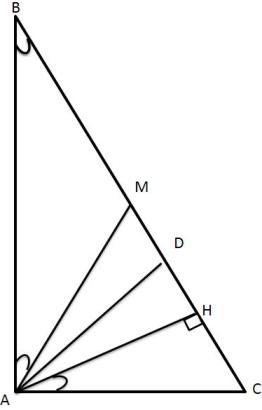
اولا میانه وارد بر وتر نصف وتر است( برای دیدن اثبات سوال ثابت کنید در مثلث قائم الزاویه ، میانه وارد بر وتر نصف وتر است را ببینید)
پس مثلث $ BAM $ متساوی الساقین است پس $ \widehat{B} = \widehat{BAM} $
حال در مثلث $ HAC $ داریم $ \widehat{C} + \widehat{CAH} =90$ اما در مثلث قائم الزاویه اولی هم $ \widehat{C} + \widehat{B} =90$ پس
$ \widehat{CAH} = \widehat{B}= \widehat{BAM} $
پس حکم ثابت می شود چون:
$$ \widehat{MAD} = \widehat{BAD} - \widehat{BAH} = \widehat{CAD} - \widehat{CAH} = \widehat{DAH} $$