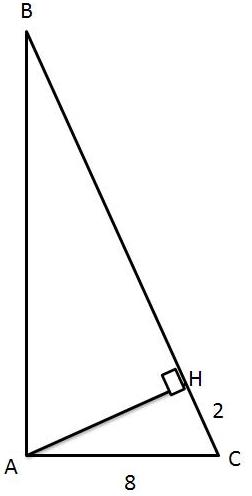
کافیست دقت کنیم که دو مثلث $ ABC $ و $ AHC $ متشابه هستند لذا اگر نسبت تشابه را بنویسم(وتر را $ x $ قرار دهیم) خواهیم داشت.
$$ \frac{BC}{AC} = \frac{AC}{HC} \Rightarrow \frac{x}{8} = \frac{8}{2} \Rightarrow x=32$$
حال طول ضلع دیگر مثلث را از فیثاغورس پیدا میکنیم و مساحت برابر خواهد بود با نصف حاصلضرب دو ضلع قائمه