محاسبه طول ضلع هشت ضلعی محاط در دایره

Question

طول ضلع هشت ضلعی محاط در دایره ای به شعاع R را برحسب R بیابید

Answer 1

$$a= \frac{360}{8}$$ $$S =8 S_{AOB}$$ $$S = \frac{ R^{2} .sina}{2}$$ $$S = \frac{8}{2} R^{2} .sin \frac{360}{8}$$ $$sin \frac{360}{8} =sin45= \frac{ \sqrt{2} }{2}$$ $$S =2 \sqrt{2} . R^{2}$$ $$S= \sqrt{2+ \sqrt{2} } . b^{2}$$ $$\sqrt{2+ \sqrt{2} } . b^{2}=2 \sqrt{2} . R^{2}$$ $$b^{2} = \frac{2 \sqrt{2} . R^{2}}{ \sqrt{2+ \sqrt{2} } }$$

Answer 2

با توجه به شکل رسم شده توسط دوستان و با رسم ارتفاع در یکی از مثلث ها شکل زیر را داریم: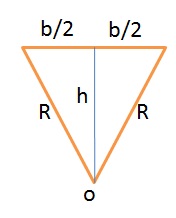

مساحت 8 مثلث برابر است با:

$$s=8( \frac{1}{2}bh)=4bh$$

از طرفی:

$$h^{2}+(\frac{b}{2})^{2}=R^{2} \Rightarrow h= \sqrt{R^{2}- \frac{b^{2}}{4}}$$ در نتیجه: $$s=4bh=4b\sqrt{R^{2}-\frac{b^{2}}{4}}$$

همچنین:

$$s =8( \frac{ R^{2} .sina= R^{2}\frac{ \sqrt{2} }{2}}{2}=R^{2}\frac{ \sqrt{2} }{4})=2 \sqrt{2} R^{2}$$

با برابر قرار دادن این دو مساحت b برحسب R به دست می آید.

Answer 3

به طور کلی طول وتری که زاویه $\alpha$ می سازد برابر است با:

$$AB=2r\sin\frac\alpha 2$$

در هشت ضلعی $\alpha=\frac{360}{8}=45$ بنابراین طول ضلع برابر است با

$$R\sin\frac{45}2=R\sin22.5$$

برای پیدا کردن $\sin 22.5$ می توانید از رابطه $\sin^2x=\frac{1-\cos 2x}2$ استفاده کنید که $x=22.5$ در اینصورت خواهیم داشت

$$\sin^2 22.5=\frac{1-\cos 45}{2}=\frac{1-\frac{\sqrt 2}2}2=\frac{2-\sqrt 2}{4}$$ بنابراین $\sin 22.5=\frac{\sqrt{2-\sqrt 2}}2$

یعنی طول ضلع برابر خواهد بود با

$$\big(\sqrt{2-\sqrt 2}\big)R$$