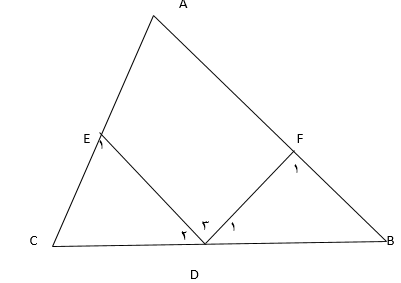
مطابق شکل و فرض مساله بنابرقضیه متساوی الساقین $F_1=D_1$ و $E_1=D_2$
بنابر مجموع زوایای داخلی مثلث:
$$\begin{align}\triangle CDE: &C+2D_2=180\tag{1}\\
\triangle BDF: & B+2D_1=180\tag{2}\\
\triangle ABC: & A+B+C=180\Rightarrow B+C=180-70=110\tag{3}\end{align}$$
با مجموع طرفین $(1),(2)$ و استفاده از $(3)$ داریم $$\underbrace{(B+C)}_{110}+2(D_1+D_2)=360$$
بنابراین $$D_1+D_2=125$$
اما $D_1,D_2,D_3$ تشکیل زاویه نیم صفحه می دهند لذا $D_3=55$.