Question

مثلث ABC و ADE متساوی الساقین هستند، ثابت کنید$\widehat{E_{1} }= \frac{ \widehat{A_{1} } }{2} $.

Comments

میشه زاویه های قائمه دو مثلث رو مشخص کنید؟

---

با عرض پوزش قائم الزاویه نیست.هر دو متساو ی الساقین اند.

Answer 1

با توجه به شکل زیر:

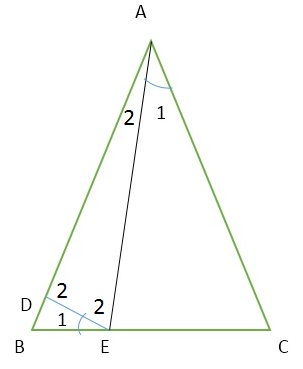
در مثلث $AEC$، زاویه $ \widehat{E_{1}} + \widehat{ E_{2} } $ زاویه خارجی مثلث است پس: $$\widehat{E_{1}} + \widehat{ E_{2} } = \widehat{A_{1}} + \widehat{C}\Rightarrow \widehat{ E_{2} } = \widehat{A_{1}} + \widehat{C}-\widehat{E_{1}}(1) $$ و در مثلث $ADE$ داریم:$ \widehat{A_{2}}+ \widehat{E_{2}}+ \widehat{D_{2} }=180 $ و $$ \widehat{E_{2}} = \widehat{D_{2} } \Rightarrow \widehat{A_{2}}=180-2\widehat{E_{2}}(2)$$

همچنین در مثلث $ABC$ داریم: $B=C(3)$

با جمع زوایای مثلث $ABE$ و قرار دادن مقادیر $ (2),(3)$ در آن داریم: $$\widehat{A_{2}}+\widehat{E_{1}} + \widehat{ E_{2} } + \widehat{B}=180 \Rightarrow 180-2\widehat{E_{2}}+\widehat{E_{1}}+\widehat{ E_{2} }+ \widehat{C}=180 $$ $$-\widehat{E_{2}}+\widehat{E_{1}}+ \widehat{C}=0\Rightarrow \widehat{E_{2}}=\widehat{E_{1}}+ \widehat{C}$$ حال با قرار دادن مقدار $ (1)$ در این عبارت داریم: $$ \widehat{A_{1}} + \widehat{C}-\widehat{E_{1}}=\widehat{E_{1}}+ \widehat{C}\Rightarrow \widehat{E_{1}}= \frac{\widehat{A_{1}}}{2} $$

Comments

سپاس از لطفتان

---

خواهش میکنم.

موفق باشید.