باتوجه به شکل زیر:
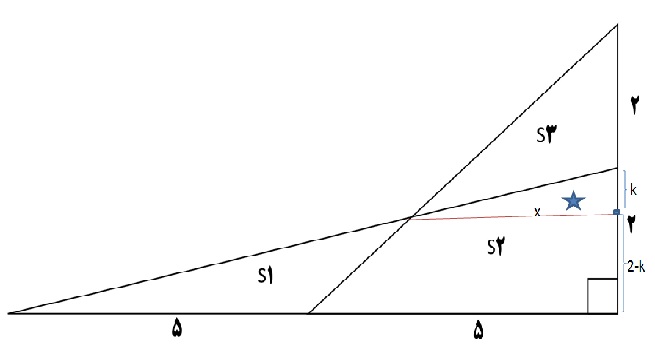
$$S1= \frac{5(2-k)}{2},S3= \frac{2x}{2}=x $$
$$S1+
S2= \frac{10 \times 2}{2}=10 =\frac{5(2-k)}{2}+ \frac{kx}{2} + \frac{(5+x)(2-k)}{2} (1)$$
$$S2+S3= \frac{4 \times 5}{2}=10=x+ \frac{kx}{2} + \frac{(5+x)(2-k)}{2} (2)$$
$$(1)=(2) \Rightarrow x=\frac{5(2-k)}{2} \Rightarrow x=5- \frac{5k}{2}(3) $$
از طرفی می توان مساحت $S1+S2$ را مجموع مساحت ذوزنقه بزرگ و مساحت مثلث $\star$ درنظر گرفت:
$$S1+
S2= \frac{(10+x)(2-k )}{2} + \frac{kx}{2}=10 \Rightarrow x=5k(4)$$
با قرار دادن $(4)$ در $(3)$داریم: $ x= \frac{10}{3} \Leftarrow k= \frac{2}{3} $
بنابراین:
$$S1= \frac{10}{3},S2=10- \frac{10}{3}=\frac{20}{3},S3=\frac{10}{3}$$