متن پرسش ۶.۳.۱۸ از شما تنها یک نمونه (مثال) خواسته است و نه تمام ایدهآلهای $I$ و $J$ با این ویژگیها را!
نکتهٔ یکم: رادیکال یک ایدهآل تکجملهای، ایدهآلی تکجملهای است و یک مولد برای آن به این روش تهیه میشود که یک مولد برای ایدهآل تکجملهای پیشین بردارید متشکل از تکجملهایها سپس تمام توانهای آن را یک کنید و تکجملهایهای جدید را درون یک مجموعهٔ جدید بگذارید. این مجموعه یک مولد برای این رادیکال میشود. اثبات آن بسیار ساده است.
پس اگر ایدهآل تکجملهای از $R$ رادیکالش برابر $\langle x,y\rangle$ شود، به این معناست که یک مولد از آن ایدهآل بودهاست که شامل دو عنصر به شکلهای $x^n$ و $y^m$ ای بودهاست برای دو عدد طبیعی $n$ و $m$ای. پس تا اینجا میدانیم که نامزدهای ما هر کدام باید دو تکجملهای به شکل یادشده داشته باشند و آزاد هستن که هر تکجملهای دیگری نیز که بخواهند در مولدشان داشته باشند.
نکتهٔ دوم: ایدهآل تکجملهای $J$ زیرمجموعهٔ ایدهآل تکجملهای $I$ است اگر و تنها اگر ناحیهٔ نموداری ایدهآل $J$ زیرمجموعهٔ ناحیهٔ نموداری ایدهآل $I$ شود که در پاسخ پرسش «خارج قسمت $a=(x_1,\cdots,x_n)R$ و یک ایده ال تکجملهای» منظور از این ناحیهها را توضیح دادهایم.
به غیر از اینکه در نمونهمان باید نکتهٔ یک و دو را رعایت کنیم باید حواسمان باشد که گوشههای این دو ایدهآل تکجملهای با یکدیگر اشتراکی نداشته باشند.
همیشه از سادهترین حالت شروع کنید و اگر چیزی نیاز بود بیافزایید. بنا به نکتهٔ یکم باید مولد دو ایدهآلمان دست کم دو عنصر به شکل توانهایی از متغیرهایمان داشته باشند پس بیاییم فعلاً با تنها همان دو عضو شروع کنیم و اگر نتوانستیم به پیروزی برسیم تکجملهایهای بیشتری در نظر بگیریم.
نکتهٔ سوم: یک ایدهآل تکجملهای به شکل $\langle x^n,y^m\rangle$ تنها دارای یک گوشه است و آن تکجملهای $x^{n-1}y^{m-1}$ است.
بنابراین با قرار دادن $I=\langle x^4,y^4\rangle$ و $I=\langle x^2,y^2\rangle$ داریم $\sqrt{I}=\sqrt{J}=\langle x,y\rangle$ و $J\subseteq I$ و
$$C_R(I)\cap C_R(J)=\{x^3y^3\}\cap\{xy\}=\emptyset$$
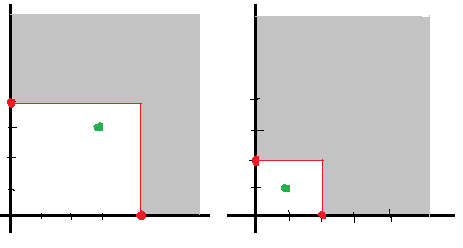
در واقع هدف پرسش این بوده است که ببینید الزامی ندارد که اگر دو ایدهآل تکجملهای دارای رادیکال یکسان باشند آنگاه گوشههایشان رابطهای داشته باشند، حتی برابر ایدهآل بیشینهٔ $\langle x_1,\cdots,x_n\rangle$ باشند و یا حتی یکی هم زیرمجموعهٔ دیگری باشد!
الزامی ندارد یعنی میتواند برقرار باشد و میتواند برقرار نباشد یا بهتر بگوئیم شرایط آورده شده برای تضمین برقراری حکم کافی نیستند.