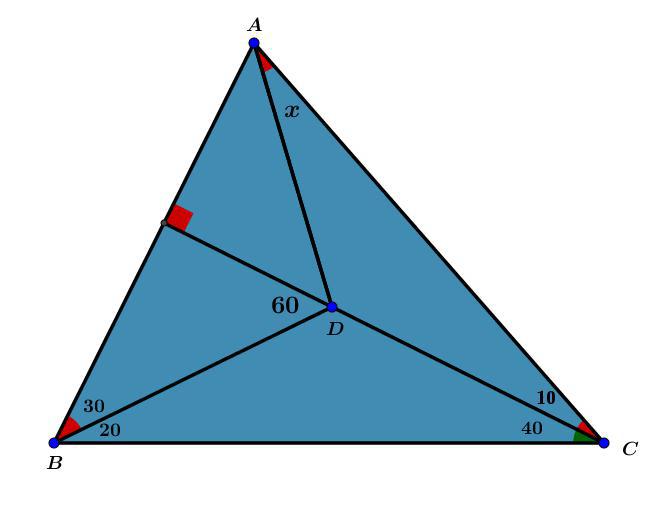
ابتدا تعریف میکنیم :
$$AB=AC=l$$
$$\triangle AEC \Rightarrow AE=l\sin 10°$$
$$\triangle BED \Rightarrow BE=\dfrac{\sqrt{3}}{2}BD \ \ , \ \ ED=\dfrac{1}{2}BD$$
$$BE=\dfrac{\sqrt{3}}{2}BD=AB-AE=l-l\sin 10°\to BD=\frac{2l(1-\sin 10°)}{\sqrt{3}}$$
$$\tan (\angle EAD)=\tan (80°-x)=\frac{ED}{AE}=\frac{1-\sin 10°}{\sqrt{3}\sin 10°}=\tan (70)$$
در نتیجه :$$\tan(80-x)=\tan(70) \\ 80-x=70 \\x^ \circ =10$$