ЩӮШ¶ЫҢЩҮ1: ЫҢЪ© ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ШӯЫҢШ·ЫҢ Ш§ШіШӘ (ШЁШұ ЫҢЪ© ШҜШ§ЫҢШұЩҮ Щ…ШӯЫҢШ· Щ…ЫҢ ШҙЩҲШҜ ЫҢШ§ ЫҢЪ© ШҜШ§ЫҢШұЩҮ ШҜШұ ШўЩҶ Щ…ШӯШ§Ш· Щ…ЫҢ ШҙЩҲШҜ) Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ЩҶЫҢЩ…ШіШ§ШІ ЩҮШ§ЫҢ ШҜШ§Ш®Щ„ЫҢ ШІЩҲШ§ЫҢШ§ЫҢ ШўЩҶ ЩҮЩ…ШұШі ШЁШ§ШҙЩҶШҜ. ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ЩҶЩӮШ·ЩҮ ЩҮЩ…ШұШіЫҢШҢ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ ЫҢ Щ…ШӯШ§Ш·ЫҢ Ш§ШіШӘ.
Ш§Ш«ШЁШ§ШӘ: ЩҒШұШ¶ Щ…ЫҢ Ъ©ЩҶЫҢЩ… ЫҢЪ© ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ШӯЫҢШ·ЫҢ Ш§ШіШӘ ЩҫШі Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ Ш§ЫҢ Ъ©ЩҮ ШҜШұ ШўЩҶ Щ…ШӯШ§Ш· ШҙШҜЩҮ Ш§ШіШӘ ЩҒШ§ШөЩ„ЩҮ ЩҮШ§ЫҢ ЫҢЪ©ШіШ§ЩҶЫҢ Ш§ШІ Ш§Ш¶Щ„Ш§Ш№ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ШҜШ§ШұШҜ (ЪҶШұШ§Шҹ) ЩҫШі Ш®Ш· ЪҜШ°ШұШ§ Ш§ШІ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ ЩҲ ЩҮШұ ШұШЈШі ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢШҢ ЩҶЫҢЩ…ШіШ§ШІ ШҜШ§Ш®Щ„ЫҢ ШІШ§ЩҲЫҢЩҮ Щ…ШӘЩҶШ§ШёШұ ШЁШ§ ШўЩҶ ШұШЈШі Ш§ШіШӘ (ШЁЩҮ Ш§ЫҢЩҶ ШЁШұЩҮШ§ЩҶ Ъ©ЩҮ ЩҶЫҢЩ…ШіШ§ШІ ЫҢЪ© ШІШ§ЩҲЫҢЩҮШҢ Щ…Ъ©Ш§ЩҶ ЩҮЩҶШҜШіЫҢ ЩҶЩӮШ§Ш·ЫҢ Ш§ШІ ШөЩҒШӯЩҮ Ш§ШіШӘ Ъ©ЩҮ ЩҒШ§ШөЩ„ЩҮ ЩҮШ§ЫҢ ЫҢЪ©ШіШ§ЩҶЫҢ Ш§ШІ Ш§Ш¶Щ„Ш§Ш№ Щ…ШӘЩҶШ§ШёШұ ШЁШ§ ШўЩҶ ШІШ§ЩҲЫҢЩҮ ШҜШ§ШұЩҶШҜ) ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ЩҶЫҢЩ…ШіШ§ШІ ЩҮШ§ЫҢ ШҜШ§Ш®Щ„ЫҢ ШІЩҲШ§ЫҢШ§ЫҢ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ШҜШұ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ ЩҮЩ…ШұШіЩҶШҜ.
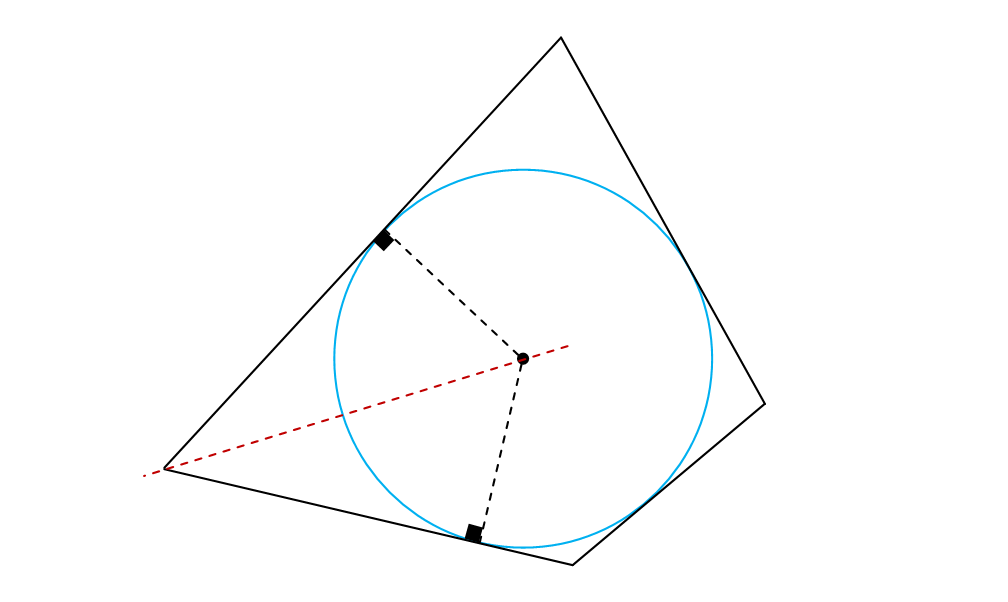
ЩҒШұШ¶ Щ…ЫҢ Ъ©ЩҶЫҢЩ… ЩҶЫҢЩ…ШіШ§ШІЩҮШ§ЫҢ ШІЩҲШ§ЫҢШ§ЫҢ ЫҢЪ© ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ ШҜШұ ЩҶЩӮШ·ЩҮ ЫҢ $o$ ЩҮЩ…ШұШіЩҶШҜ. ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ЩҶЩӮШ·ЩҮ ЫҢ $o$ ЩҒШ§ШөЩ„ЩҮ ЩҮШ§ЫҢ ЫҢЪ©ШіШ§ЩҶЫҢ Щ…Ш«Щ„ $d$ Ш§ШІ Ш§Ш¶Щ„Ш§Ш№ ЪҶЩҶШҜШ¶Щ„Ш№ЫҢ ШҜШ§ШұШҜ. ЩҫШі ШҜШ§ЫҢШұЩҮ $C(o,d)$ ШҜШұ ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ШӯШ§Ш· Ш§ШіШӘ ЩҲ ЩӮШ¶ЫҢЩҮ Ш§Ш«ШЁШ§ШӘ Щ…ЫҢ ШҙЩҲШҜ.
ЩӮШ¶ЫҢЩҮ2: ЫҢЪ© ЪҶЩҶШҜ Ш¶Щ„Ш№ЫҢ Щ…ШӯШ§Ш·ЫҢ Ш§ШіШӘ (ЫҢЪ© ШҜШ§ЫҢШұЩҮ ШЁШұ ШўЩҶ Щ…ШӯЫҢШ· Щ…ЫҢ ШҙЩҲШҜ ЫҢШ§ ШҜШұ ЫҢЪ© ШҜШ§ЫҢШұЩҮ Щ…ШӯШ§Ш· Щ…ЫҢ ШҙЩҲШҜ) Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ Ш№Щ…ЩҲШҜ Щ…ЩҶШөЩҒ ЩҮШ§ЫҢ Ш§Ш¶Щ„Ш§Ш№ ШўЩҶ ЩҮЩ…ШұШі ШЁШ§ШҙЩҶШҜ. ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ЩҶЩӮШ·ЩҮ ЩҮЩ…ШұШіЫҢШҢ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ ЫҢ Щ…ШӯЫҢШ·ЫҢ Ш§ШіШӘ.
ШҜШұШіШӘЫҢ ЩӮШ¶ЫҢЩҮ ЩҒЩҲЩӮ Щ…ШҙШ§ШЁЩҮ ЩӮШ¶ЫҢЩҮ1 Ш§Ш«ШЁШ§ШӘ Щ…ЫҢ ШҙЩҲШҜ.