به صورت کلی میخواهیم در مورد بیشینه وکمینه تابع در بازه بپردازیم.مخصوصا نقاط های انتهایی و بازه .
ابتدا همسایگی متقارن $ a $ وهمسایگی چپ و راست $a$ با شکل نشان میدهیم .
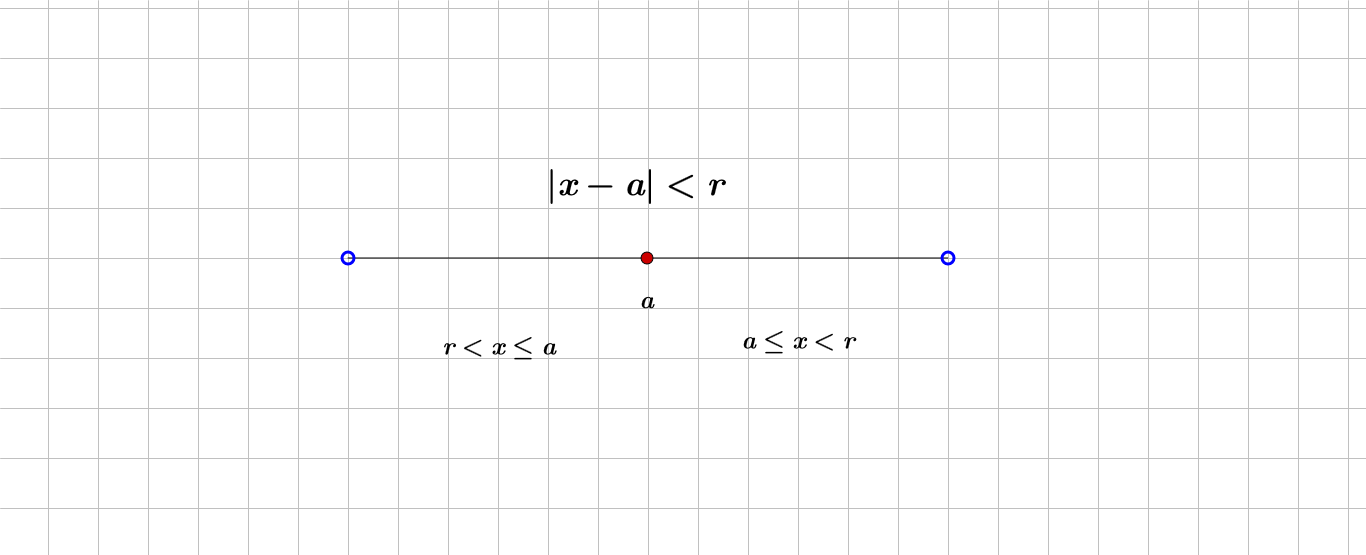
تابع حقیقی $ f $ رو درنظر بگیرید . و فرض میکنیم $S \subseteq D_{f} $ و $c \in S$ باشد در این صورت
$ f(c) $:
ماکزیمم مطلق $ f $ بر $S $ است اگر
$$ \forall x \in S \longrightarrow f(c) \geq f(x)$$
$ f(c) $:
مینیمم مطلق $ f $ بر $ S $ است اگر
$$ \forall x \in S \longrightarrow f(c) \leq f(x) $$
$ f(c) $:
ماکزیمم نسبی $ f $ بر $ S $ است اگر
$$ \forall x \in ( |x-c|< r ) \in S \longrightarrow f(c) \geq f(x) $$
$ f(c) $:
مینیمم نسبی $ f $ بر $ S $ است اگر
$$ \forall x \in ( |x-c|< r ) \in S \longrightarrow f(c) \leq f(x) $$
حال چند حالت پیش می آید .
$S=(a,b)$ : در این حالت نقاط انتهایی یعنی$a,b$ نه ماکزیمم مطلق ونسبی و نه مینیمم مطلق ونسبی هستند.!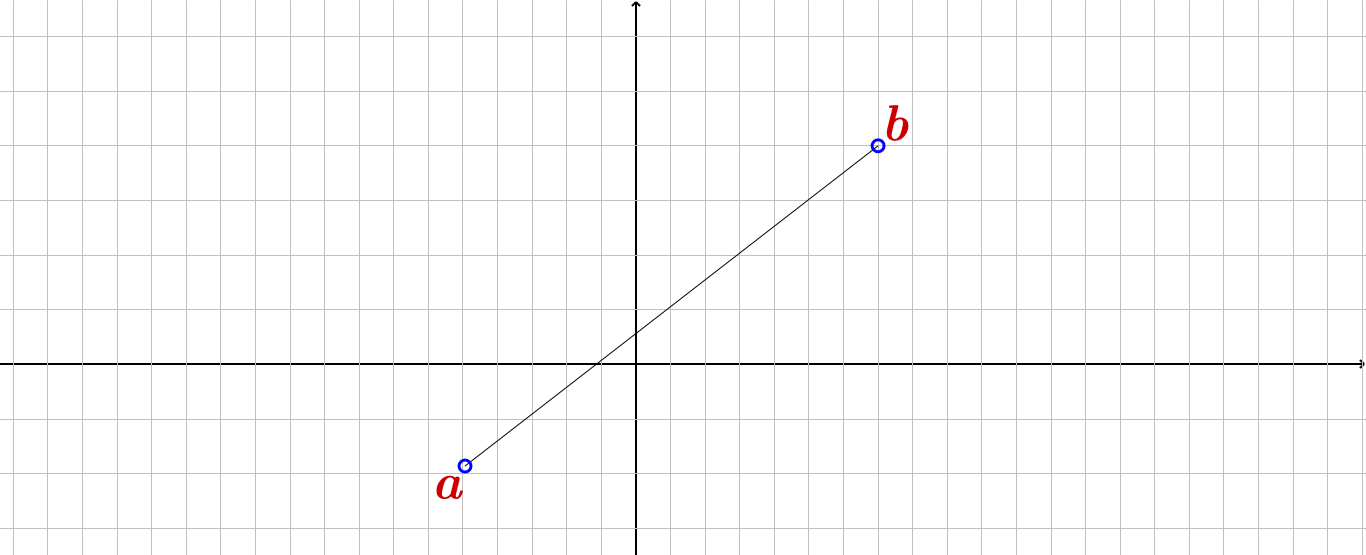
$S= [a,b) $ : در این حالت (ممکن) است$a$ ماکزیمم مطلق یا نسبی یا مینیمم مطلق یا نسبی باشند .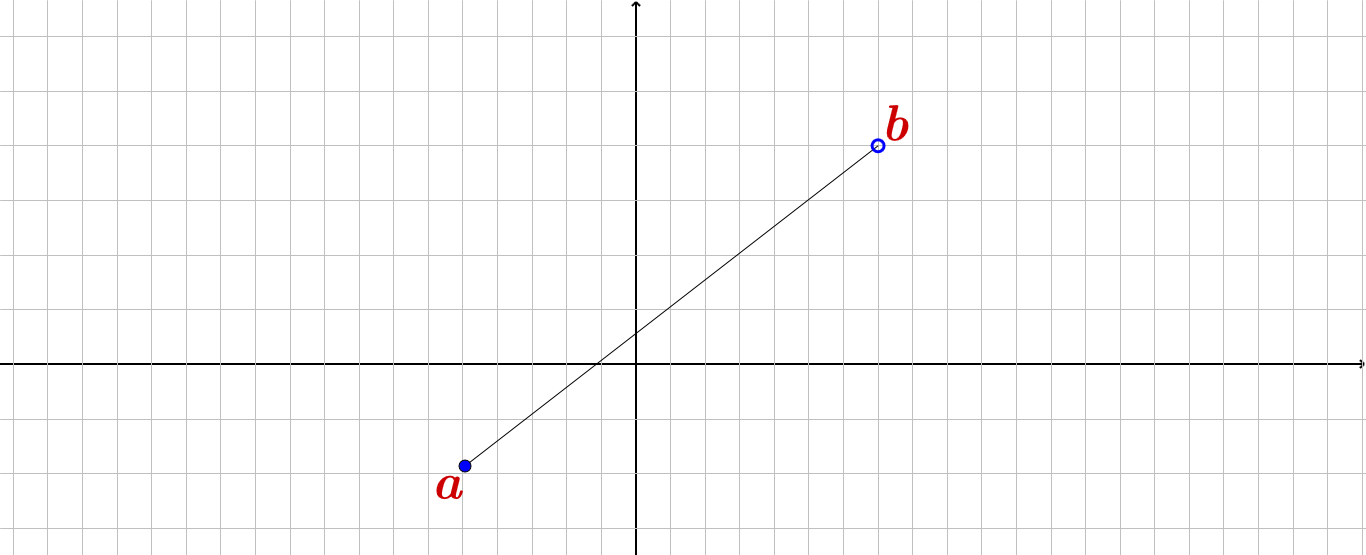
$S= (a,b]$ : در این حالت (ممکن) است$a$ ماکزیمم مطلق یا نسبی یا مینیمم مطلق یا نسبی باشند .!
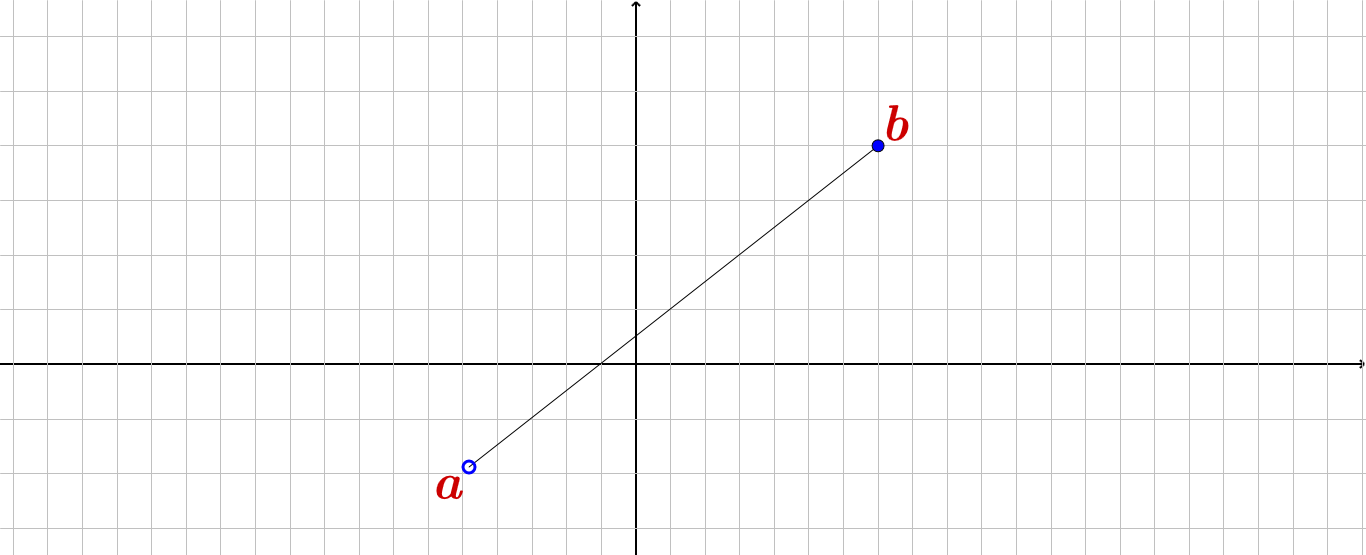
$S= [a,b]$ :در این حالت (ممکن) است$a,b$ ماکزیمم مطلق یا نسبی یا مینیمم مطلق یا نسبی باشند .!
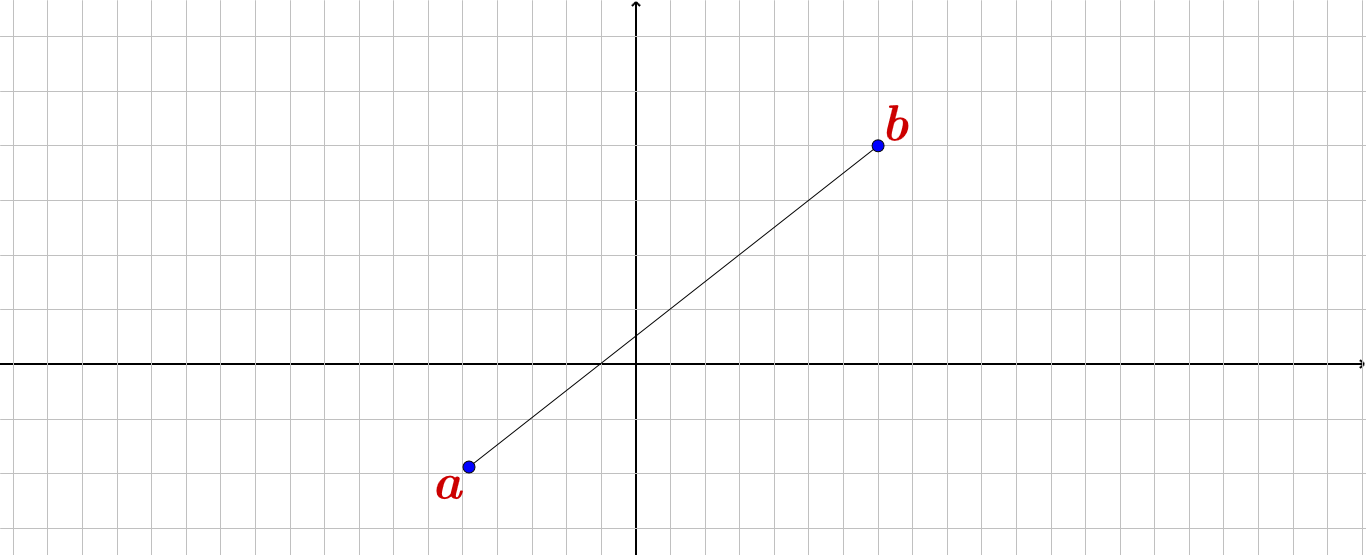
$S= [a, +\infty )$ : در این حالت (ممکن) است$a$ یا مینیمم مطلق و نسبی یا ماکزیمم مطلق نسبی باشند .!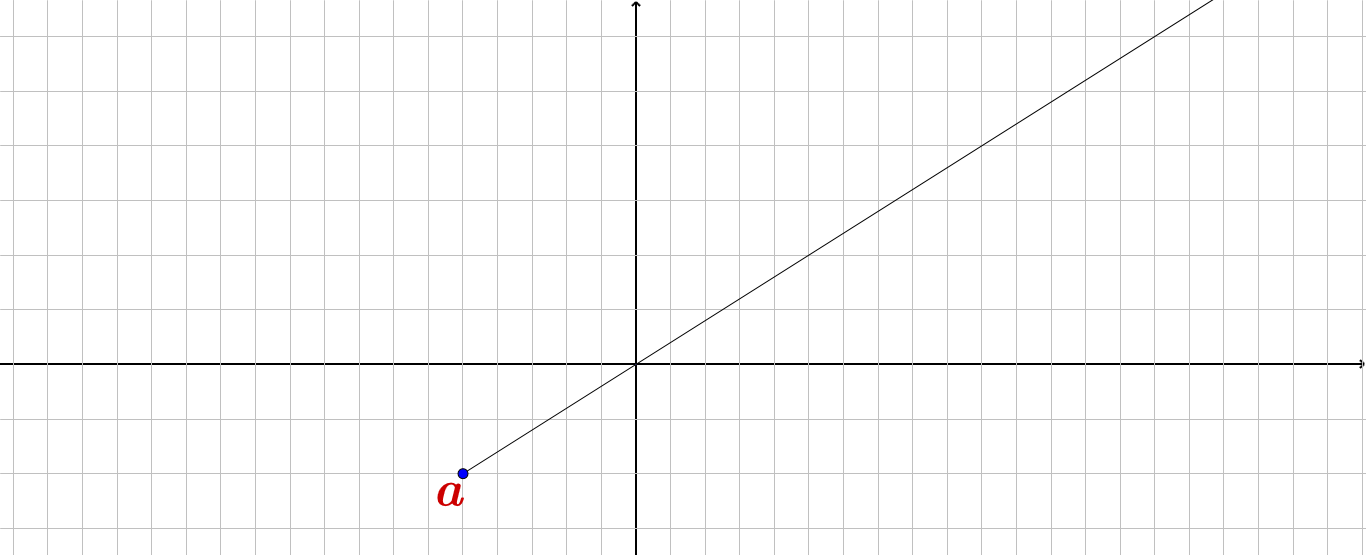
$S= (-\infty ,b] )$ : در این حالت (ممکن) است$a$ یا ماکزیمم مطلق و نسبی یا مینیمم مطلق و نسبی باشند .!!
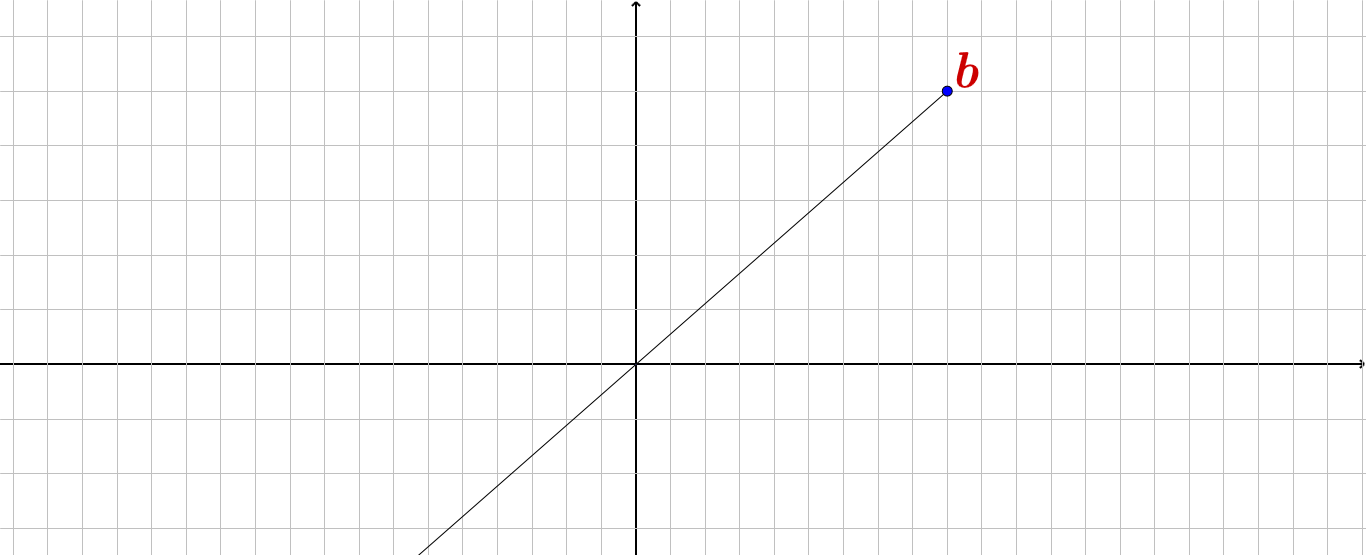
$S= (-\infty ,b ) or (a,+\infty)$ : در این دو حالت ممکن نیست $ a,b $ ماکزیمم مطلق یا نسبی و مینیمم مطلق یا نسبی باشد .
حالاتی هم پیش می آید که باعث سوال میشود. تابع زیر رو در نطر بگیرید: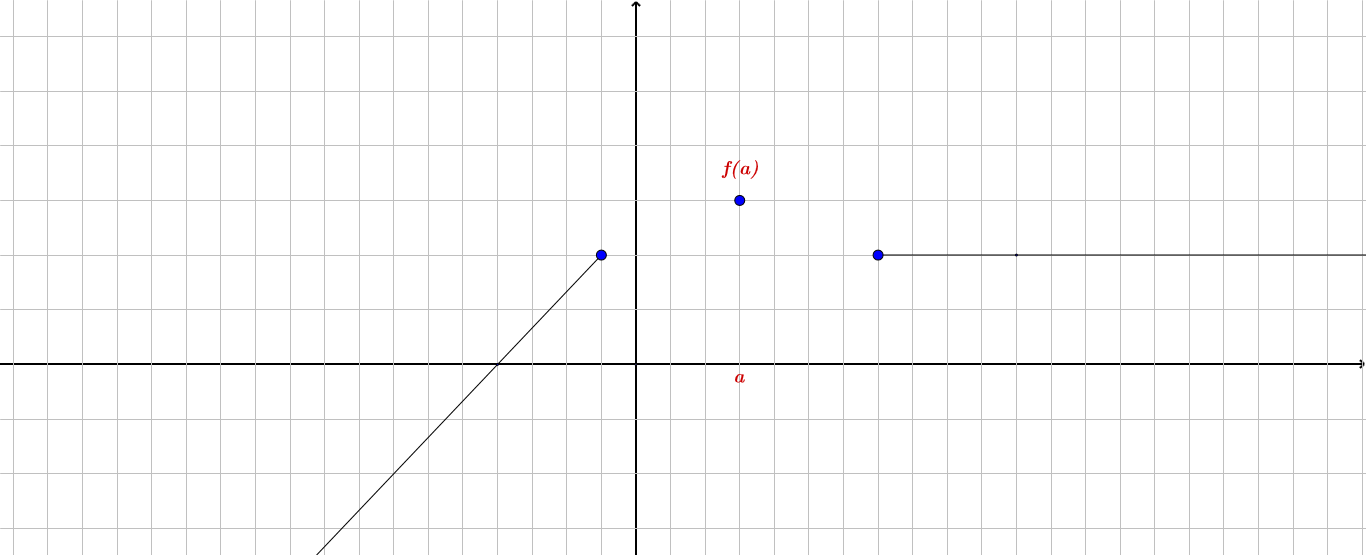
در این تابع نقطه $(a, f(a))$ ماکزیمم مطلق و نسبی است .چرا ؟ زیرا
$ \forall x \in S \in D_f \longrightarrow f(a) \geq f(x) $بنابر این ماکزیمم مطلق است .
$ \forall x \in ( |x-a|< r ) = a \in S \longrightarrow f(a) \geq f(x) $ بنابر این ماکزیمم نسبی است .
$( \forall x \in ( |x-a|< r ) \in S)$ برابر میشود با $a$
تابع زیر رو در نطر بگیرید: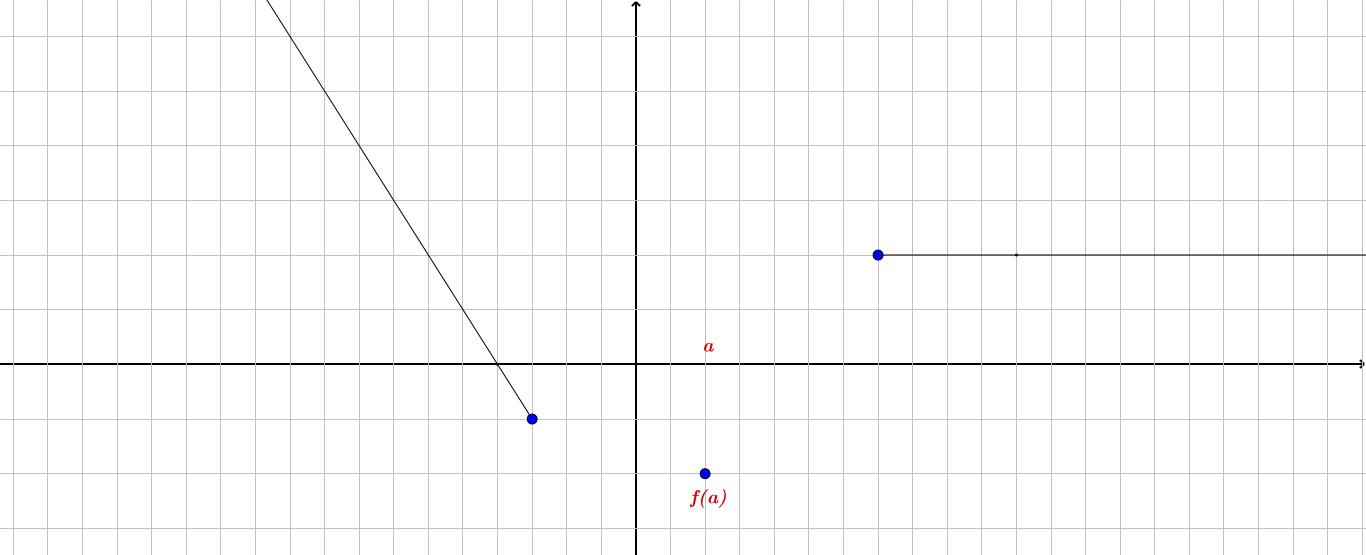
در این تابع نقطه $ (a, f(a)) $ مینیمم مطلق و نسبی است .چرا ؟ زیرا
$ \forall x \in S \in D_f \longrightarrow f(a) \leq f(x) $بنابر این مینیمم مطلق است .
$ \forall x \in ( |x-a|< r ) = a \in S \longrightarrow f(a) \leq f(x) $ بنابر این مینیمم نسبی است .
$ (\forall x \in ( |x-a|< r ) \in S)$ برابر میشود با $a$
بنابر این هر ماکزیمم مطلق یا میینمم مطلق . ماکزیمم نسبی و مینیمم نسبی محسوب میشود .
ولی هر ماکزیمم نسبی و مینیمم نسبی ماکزیمم مطلق یا مینیمم مطلق محسوب نمیشود .
(در شکل هایی که رسم شده برای این بخش بیشتر تابع خطی رو بحث زیرا هدف ما تنها نقاط انتهایی بازه بود )