احتمالا میدانید که برای یافتن اکسترممهای نسبی تابعتان باید مکانهایی که مشتقهای جزئی تعریف نمیشوند یا همگیشان با هم صرف هستند را بگردید. نخست توجه دارید که دامنهٔ تابعتان دو خط $x=0$ و $y=0$ را شامل نمیشود. بعلاوه تابعتان مشتقپذیر است، پس اکنون میماند بررسی مکانهایی که $f'_x=f'_y=0$. اینکه این دستگاه تنها یک پاسخ دارد و آن هم نقطهٔ $(\frac{-1}{4},16)$ است را باید بتوانید به سادگی محاسبه کنید. اکنون میماند تشخیص اینکه این نقطه کمینهٔ نسبی، یا بیشینهٔ نسبی، یا از هیچ یک از این دو گونه است. برای این کار باید از تعمیم قضیهٔ مشتق دوم برای تعیین گونهٔ اکسترمم استفاده کنید. این قضیه میگوید ماتریس هِسیَن تابعتان را تشکیل دهید یعنی $H=\begin{bmatrix}\frac{\partial^2 f}{\partial x_i\partial x_j}\end{bmatrix}_{1\leq i,j\leq n}$ که $n$ تعداد متغیرهای تابعتان است. پس در اینجا داریم
$$H=\begin{bmatrix}
\frac{\partial}{\partial x}(\frac{\partial f}{\partial x}) & \frac{\partial}{\partial y}(\frac{\partial f}{\partial x})\\
\frac{\partial}{\partial x}(\frac{\partial f}{\partial y}) & \frac{\partial}{\partial y}(\frac{\partial f}{\partial y})
\end{bmatrix}=\begin{bmatrix}
\frac{2}{x^3} & 1\\
1 & \frac{-128}{y^3}
\end{bmatrix}$$
اکنون نقطهای که مشتقهای اول همگی صفر شدهاند را در این ماتریس جایگذاری کنید. یعنی در اینجا باید قرار دهیم $x=-\frac{1}{4}$ و $y=16$.
$$\begin{bmatrix}
-128 & 1\\
1 & \frac{-1}{32}
\end{bmatrix}$$
اکنون مقدارهای ویژهٔ آن را بیابید.
- اگر همهٔ مقدار ویژهها مثبت بودند، آنگاه تابعتان در این نقطه کمینهٔ نسبی دارد.
- اگر همهٔ مقدار ویژهها منفی بودند، آنگاه تابعتان در این نقطه بیشینهٔ نسبی دارد.
- اگر هم مقدار ویژهٔ مثبت و هم مقدار ویژهٔ منفی داشت، نقطهتان یک نقطهٔ زینی است.
در غیر از این سه مورد، این آزمون بینتیجه است.
مقدارهای ویژه ریشههای چندجملهای سرشتنما (مشخصه) بودند که برای یک ماتریس دو در دو به شکل $a^2-{\rm tr}(A)+\det(A)$ نوشته میشد. پس در اینجا چندجملهای سرشتنمایمان به شکل زیر است.
$$a^2+(128+\frac{1}{32})a+4$$
روشن است که $\Delta=(128+\frac{1}{32})^2-4(1)(4)$ عددی مثبت میشود پس چندجملهای سرشتنمایمان دو ریشهٔ حقیقی دارد. و چون جملهثابت مثبت است این دو ریشه همعلامت هستند و چون ضریب جملهٔ درجهیک مثبت است پس علامتشان منفی است. یعنی دو مقدار ویژهٔ منفی داریم پس حالت شمارهٔ ۲ از قضیه رخ دادهاست و نقطهٔ مورد بحث یک بیشینهٔ نسبی است.
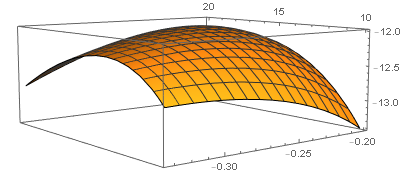
برای امتحان میتوانید شکل تابع را در همسایگی این نقطه در زیر ببینید (شکل کشیدهشده بوسیلهٔ نرمافزار Mathematica).
Plot3D[1/x - 64/y + x*y, {x, -1/5, -1/3}, {y, 10, 20}]