ШӘШ§ШЁШ№ ШҜШұШ¬ЩҮ ШұШЁШ·ЫҢ ШЁЩҮ ШӘШ§ШЁШ№ ЩҲШІЩҶ ЩҶШҜШ§ШұШҜШҢ ШЁШұШ§ЫҢ ЩҮЩ…ЫҢЩҶ Щ…Ш·Щ„ШЁ ШІШ§ШҰШҜЫҢ ШҜШұ ЩҫШұШіШҙвҖҢШӘШ§ЩҶ Ш§ШҙШ§ШұЩҮ Ъ©ШұШҜЩҮвҖҢШ§ЫҢШҜ. ЪҜШұШ§ЩҒ ШЁЫҢвҖҢШ¬ЩҮШӘ Ъ©ЩҮ ЫҢШ§Щ„ Щ…ЩҲШ§ШІЫҢ ЩҶЫҢШІ ЩҶШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ ШұШ§ ЪҜШұШ§ЩҒ ШіШ§ШҜЩҮ Щ…ЫҢвҖҢЪҜЩҲЫҢЩҶШҜ (ШҜЩҲ ЫҢШ§Щ„ ШұШ§ Щ…ЩҲШ§ШІЫҢ ЪҜЩҲШҰЫҢЩ… ЩҮШұ ЪҜШ§ЩҮ ШЁЫҢЩҶ ШҜЩҲ ЪҜШұЩҮЩ” ЫҢЪ©ШіШ§ЩҶ ШЁШ§ШҙЩҶШҜ). ЩҫШұШіШҙ ШҙЩ…Ш§ ШҜШұ ЩҲШ§ЩӮШ№ ЩҫЫҢШұШ§Щ…ЩҲЩҶ ЪҜШұШ§ЩҒвҖҢЩҮШ§ЫҢ ШіШ§ШҜЩҮ Ш§ШіШӘ. ШЁШұШ§ЫҢ ЪҶЩҶЫҢЩҶ ЪҜШұШ§ЩҒвҖҢЩҮШ§ЫҢЫҢШҢ ЩҲШІЩҶ ЫҢЪ© ЫҢШ§Щ„ ШұШ§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁШ§ ШӘШ§ШЁШ№ЫҢ Щ…Ш§ЩҶЩҶШҜ $f(x,y)$ Ъ©ЩҮ ШҜШ§Щ…ЩҶЩҮЩ” ШўЩҶ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” ЫҢШ§Щ„вҖҢЩҮШ§ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ШІЫҢШұЩ…Ш¬Щ…ЩҲШ№ЩҮЩ” ШӯШ§ШөЩ„вҖҢШ¶ШұШЁ ШҜЪ©Ш§ШұШӘЫҢ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” ЪҜШұЩҮвҖҢЩҮШ§ ШҜШұ Ш®ЩҲШҜШҙ Ш§ШіШӘ ЩҲ ШЁШұШҜ ШўЩҶ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” ЩҲШІЩҶвҖҢЪҜШ°Ш§Шұ Ш§ШіШӘШҢ ЩҶЩ…Ш§ЫҢШҙ ШҜШ§ШҜ. ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Ш§ЫҢЩҶЪ©ЩҮ ЩҲШІЩҶ ЫҢШ§Щ„ ШЁЫҢЩҶ ЪҜШұЩҮЩ” $A$ ЩҲ ЪҜШұЩҮЩ” $B$ ШЁШұШ§ШЁШұ Ыі ШЁШ§ШҙШҜ ШұШ§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ Ш§ЫҢЩҶ ШҙЪ©Щ„ ШЁЫҢШ§ЩҶ Ъ©ШұШҜ Ъ©ЩҮ $f(A,B)=3$.
Ш§Ъ©ЩҶЩҲЩҶ Щ…Ш§ШӘШұЫҢШіЫҢ Ъ©ЩҮ ШўЩҲШұШҜЩҮвҖҢШ§ЫҢШҜ ШҜЩӮЫҢЩӮШ§ Щ…Ш§ШӘШұЫҢШі ЩҮЩ…ШіШ§ЫҢЪҜЫҢ Ш§ШіШӘ adjacency matrix Ъ©ЩҮ ШҜШұШ§ЫҢЩҮЩ” $(i,j)$-Ш§ЩҸЩ… ШўЩҶ ШІЩ…Ш§ЩҶЫҢ ЫҢЪ© ШЁЩҲШҜ Ъ©ЩҮ ШЁЫҢЩҶ ШҜЩҲ ЪҜШұЩҮЩ” $i$Ш§ЩҸЩ… ЩҲ $j$Ш§ЩҸЩ… ЫҢШ§Щ„ЫҢ ШЁШ§ШҙШҜ ЩҲ ШҜШұ ШәЫҢШұ Ш§ЫҢЩҶШөЩҲШұШӘ ШөЩҒШұ Щ…ЫҢвҖҢШЁЩҲШҜ. Ш§Щ…Ш§ ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ШЁЩҮ Ш¬Ш§ЫҢ ЫҢЪ©ШҢ Щ…ЩӮШҜШ§Шұ $f(i,j)$ ШұШ§ ЩӮШұШ§Шұ Щ…ЫҢвҖҢШҜЩҮЫҢШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Щ…Ш§ШӘШұЫҢШі ЩҮЩ…ШіШ§ЫҢЪҜЫҢ ШЁШұШ§ЫҢ ЫҢЪ© ЪҜШұШ§ЩҒ ШіШ§ШҜЩҮ ЩҮЩ…ЫҢШҙЩҮ Щ…ШӘЩӮШ§ШұЩҶ ЩҲ ШұЩҲЫҢ ЩӮШ·Шұ Ш§ШөЩ„ЫҢвҖҢШ§Шҙ ШөЩҒШұ Ш§ШіШӘ. ШҜЩ„ЫҢЩ„ ШўЩҶ ЩҶЫҢШІ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ЪҶЩҲЩҶ Ш·ЩҲЩӮЩҮ ЩҶШҜШ§ШұЫҢШҜ ШЁЫҢЩҶ ЫҢЪ© ЪҜШұЩҮ ЩҲ Ш®ЩҲШҜШҙ ЫҢШ§Щ„ЫҢ ЩҶЫҢШіШӘ. ШЁШ№Щ„Ш§ЩҲЩҮ ЪҶЩҲЩҶ ЫҢШ§Щ„вҖҢЩҮШ§ ШЁЫҢвҖҢШ¬ЩҮШӘ ЩҮШіШӘЩҶШҜШҢ ЫҢЪ© ЫҢШ§Щ„ Ъ©ЩҮ ШЁЫҢЩҶ $i$ ЩҲ $j$ ШЁШ§ШҙШҜ ШЁЫҢЩҶ $j$ ЩҲ $i$ ЩҶЫҢШІ ЩҮШіШӘ. ШҜШұ ЩҲШ§ЩӮШ№ ШҜЩҲ Ш§ЩҶШӘЩҮШ§ЫҢ ЫҢЪ© ЫҢШ§Щ„ ШұШ§ Ш§ШІ ЩҮШұ ШіЩ…ШӘ ЩҶЪҜШ§ЩҮ Ъ©ЩҶЫҢШҜ ЩҒШұЩӮЫҢ ЩҶШҜШ§ШұШҜ.
ШҙЪ©Щ„ ЪҜШұШ§ЩҒ ШіШ§ШҜЩҮЩ” ЩҲШІЩҶвҖҢШҜШ§Шұ Щ…ШұШЁЩҲШ· ШЁЩҮ Щ…Ш§ШӘШұЫҢШі ЩҮЩ…ШіШ§ЫҢЪҜЫҢ (ШЁШ§ ШҜШұШ§ЫҢЩҮвҖҢЩҮШ§ЫҢ ЩҲШІЩҶ)ШӘШ§ЩҶ ШҜШұ ШІЫҢШұ ШўЩ…ШҜЩҮвҖҢШ§ШіШӘ:
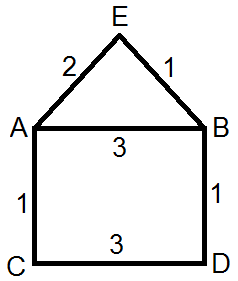
ШҜЩҲШЁШ§ШұЩҮ ШӘШЈЪ©ЫҢШҜ Щ…ЫҢвҖҢЪ©ЩҶЩ… Ъ©ЩҮ ЫҢЪ© ЪҜШұШ§ЩҒ ШҜШ§ШұШ§ЫҢ ЫҢШ§Щ„ Щ…ЩҲШ§ШІЫҢ ШӯШӘЫҢ Ш§ЪҜШұ ШЁЫҢвҖҢШ¬ЩҮШӘ ЩҲ ШЁЫҢвҖҢШ·ЩҲЩӮЩҮ ШЁШ§ШҙШҜ ШұШ§ ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁШ§ Ш§ЫҢЩҶ Ш§ЫҢШҜЩҮ ЩҲШІЩҶвҖҢЪҜШ°Ш§ШұЫҢ Ъ©ШұШҜ! ЩҫШі ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ ШҙЪ©Щ„ЫҢ Ъ©ЩҮ ШӘЩҲШ¶ЫҢШӯ ШҜШ§ШҜЩҮвҖҢШҙШҜШҢ ЫҢШ§Щ„вҖҢЩҮШ§ЫҢШҙ ШұШ§ ЩҲШІЩҶвҖҢЪҜШ°Ш§ШұЫҢ Ъ©ШұШҜ. ШІЫҢШұШ§ Ъ©ЩҮ ШЁЫҢЩҶ ШҜЩҲ ЪҜШұЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ЪҶЩҶШҜ ЫҢШ§Щ„ ШЁШ§ШҙШҜ ЩҲ ЫҢЪ© ЫҢШ§Щ„ ШЁШ§ ШӘЩҶЩҮШ§ Ш§ШҙШ§ШұЩҮ Ъ©ШұШҜЩҶ ШЁЩҮ ЪҜШұЩҮвҖҢЩҮШ§ЫҢ ШҜЩҲ Ш§ЩҶШӘЩҮШ§ЫҢШҙ ШЁЩҮ Ш·ЩҲШұ ЫҢЪ©ШӘШ§ Щ…ШҙШ®Шө ЩҶЩ…ЫҢвҖҢШҙЩҲШҜ.