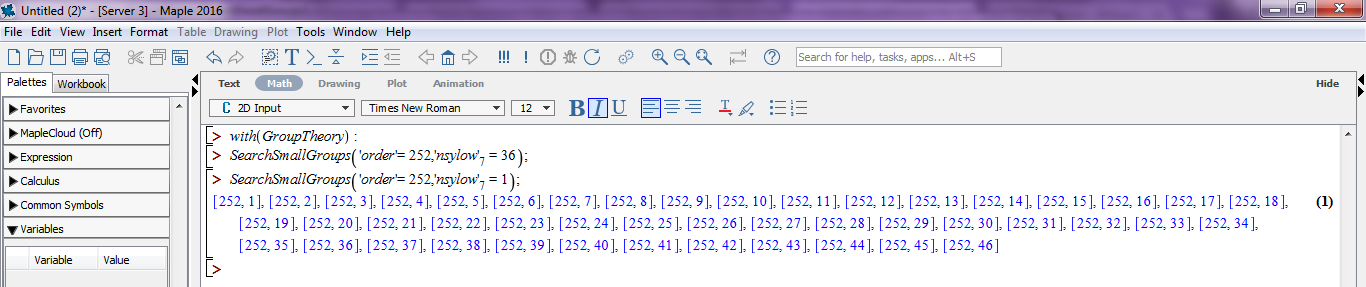
چون $252=7\times 3^2\times 2^2$ است پس ۷-زیرگروههای سیلو، زیرگروههای از مرتبهٔ ۷ هستند. چون تعداد این گروهها باید شاخصشان یعنی $\frac{252}{7}=36$ را بشمارد و بعلاوه به پیمانهٔ ۷ همنهشت با یک باشد پس دو حالت بیشتر ندارد یا یک است یا سیوشش. اگر یک بشود یک زیرگروه نرمال نیز میشود. بنابراین پرسش شما همارز این است که ثابت کنید هیچ گروهی از مرتبهٔ ۲۵۲ دارای زیرگروه هفتعضوی نرمال نیست. برای اثباتش باید از ۲-زیرگروه و ۳-زیرگروههای سیلو نیز کمک بگیرید. به هر حال در زیر به جای اثبات توضیحی که مطمئنا شما آن را ترجیح میدهید، اثبات نرمافزاری گذاشتهام. با استفاده از بستهٔ نظریهٔ گروه نرمافزار میپل میتوانید از نرمافزار بخواهید تمام زیرگروههای متمایز تا حد یکریختی از یک مرتبهٔ نه بزرگ را محاسبه و یک سری ویژگیها را برایتان چک کند. البته از قضایایی که شما نیز استفاده میکنید نیز برای کاستن تعداد محاسبات و دور زدن نیز استفاده میکند. برای نمونه در زیر خواستهایم که گروههای از مرتبهٔ ۲۵۲ که دارای ۳۶ ۷-زیرگروه سیلو هستند را معرفی کند که هیچ خروجیای ندادهاست یعنی وجود ندارد. سپس با یک ۷-زیرگروه سیلو را خواستهایم که هر ۴۶ گروه ۲۵۲ عضوی را به عنوان خروجی برگرداندهاست.