با سلام خوش آمدید .
ابتدا با تعریف مشتق شروع میکنیم .
فرص کنید $x=a$ :
1-) در دامنه تابع $f$ باشد .
2-) یک نقطه حدی تابع $f$ باشد .
آنگاه تعریف میکنیم
$$ \lim_{x \rightarrow a} \frac{f(x)-f(a)}{x-a} :=\dfrac{d}{dx}f(a)=f'(a)$$
اگر این حد موجود باشد .
در نتیجه اگر یک نقطه موجود باشه که در دو شرط $(1),(2)$ صدق کنه میتوان مشتق برای آن نقطه تعریف کنیم . که ممکنه مشتق آن موجود باشد یا مشتق آن موجود نباشد . پس تمیز قائل بشید بین :
الف) مشتق تعریف نمیشود در یک نقطه .
ب) مشتق وجود ندارد در یک نقطه .
مثال :
تابع$f(x)=|x|$ در نظر بگیرید . آیا در نقطه $x=0$ مشتق تعریف میشود ؟ و اگر تعریف میشود .آیا مشتق آن وجود دارد ؟
میدانیم که $x=0$ برای تابع$f$ نقطه حدی است و در دامنه تابع هم وجود دارد . در نتیجه مشتق تعریف میشود .
حال به دنبال آن هستیم که ببینیم مشتق آن وجود دارد یا خیر .
$$ \lim_{x \rightarrow 0} \frac{f(x)-f(0)}{x-0}=\lim_{x \rightarrow 0} \frac{|x|}{x} $$
میدانیم که $\frac{|x|}{x}$ تابع علامته . نمودارشو در نظر بگیرید :
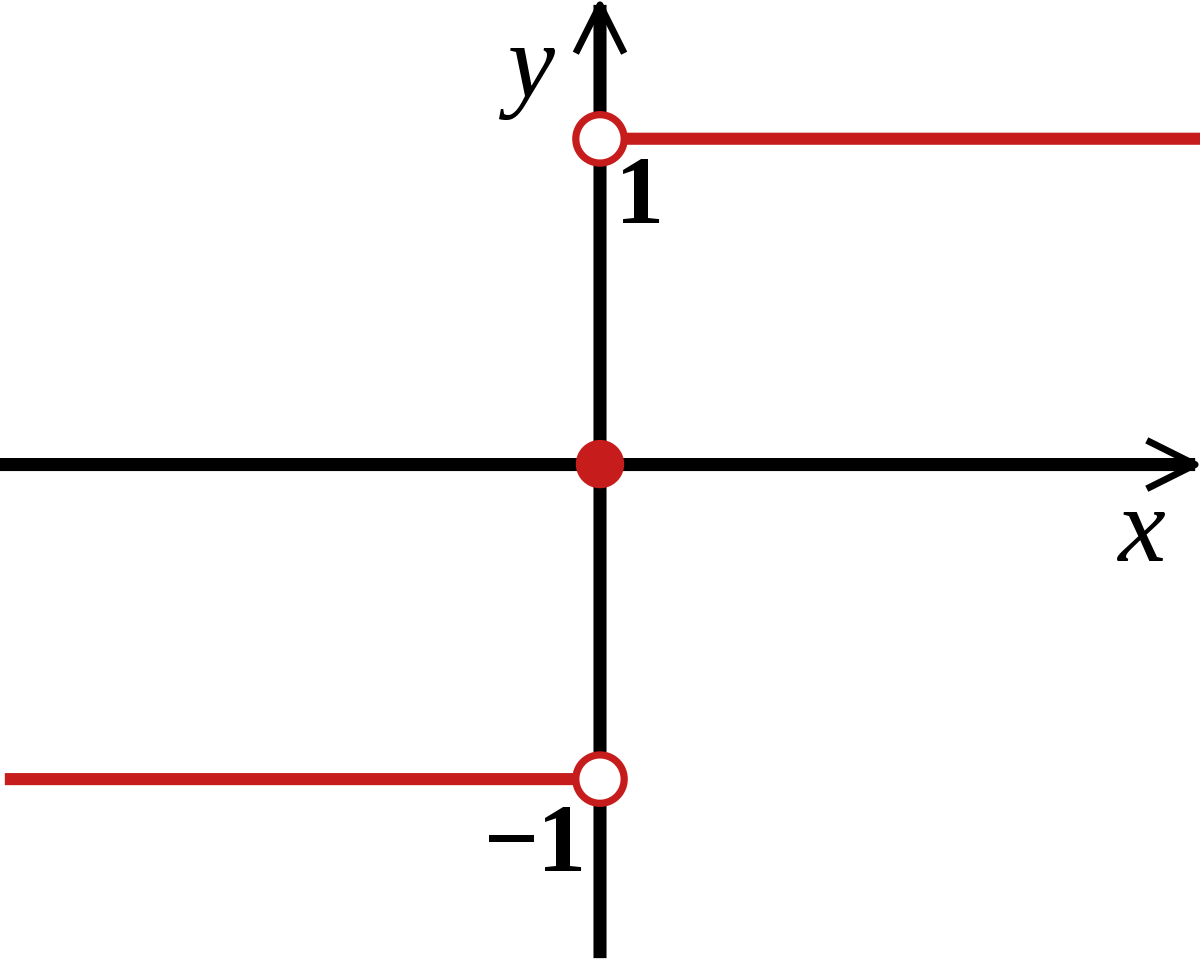
مشتق چپ و راست آن باهم یکی نیست در نتیجه تابع $f$ در نقطه $x=0$
مشتق ندارد .