هم ارزی یا هم توانی دو مجموعه ی $A$و $B$ یعنی یک تابع یک به یک و پوشا بین عناصر آنها وجود داشته باشد. به عنوان مثال $\{1,2,3\}$ با مجموعه ی $\{a, b,c\}$ همتوان است چرا که می توانیم تناظری مثل
$$1\to a\\ 2\to b\\ 3\to c$$
بین آنها یافت.
یا مثلا $\{0,1,2,3,\cdots\}$ با $\{0,2,4,6,\cdots\}$ همتوان است چرا که تناظر $$0\to 0\\ 1\to 2\\ 2\to 4\\ \vdots \\ k\to 2k\\ \vdots$$
بین آنها را می توانیم در نظر بگیریم.
واضح است که هر دوبازه باز، همتوان هستند به عنوان مثال $(0,1)$ را با $(5,8)$ در نظر بگیرید می توانیم به هر $x\in (0,1)$ عنصر $3x+5$ را نسبت داد. پس واضح است هر دو بازه $(a,b)$ و $(c,d)$ همتوان هستند.
به همین ترتیب می توان نشان داد بازه های به صورت $(a,b]$ و $(c,d]$ نیز همتوان هستند. همچنین بازه های $[a,b)$ و $[c,d)$ و دو بازه بسته هم همینطور.
اما چرا مثلا بازه ای مثل $[0,1]$ با بازه ای مثل $(0,1]$ همتوان است؟
تناظر را به صورت زیر در نظر بگیرید:
$$0\to 1\\ 1\to \frac 12\\ \frac 12\to \frac 13\\ \vdots \\ \frac 1n\to \frac 1{n+1}\\ \vdots $$
و غیر از اینها را به خودش بفرستد.
به طور مشابه می توانید ثابت کنید که چرا $[0,1]$ و $(0,1]$ و $(0,1)$ هم توان هستند.
که این هم خود نشان می دهد که چرا همه بازه ها با یکدیگر هم توان اند مثل $(a, b), (a, b], [a, b), [a, b]$ .
حال کافی است فقط نشان دهیم که $(a,b)$ با $\mathbb R$ هم ارز است. چون $(a, b)$ با $(-\frac\pi 2,\frac\pi 2)$ هم ارز است کافی است به هر $x\in (-\frac\pi 2,\frac\pi 2)$ عنصر $ \tan x\in \mathbb R $ را نسبت داد.
البته این تناظر را با شکل هم می توان به صورت زیر متصور شد:
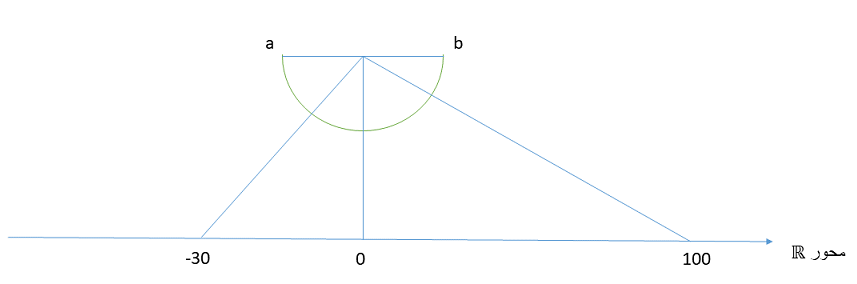
به این ترتیب که بازه ی $(a,b)$ با نیم دایره هم توان است چرا که به هر نقطه روی دایره می توان بر بازه عمود کرده و پای عمود را به آن نظیر کرد. حال ادعا می کنیم که نیم دایره با کل اعداد حقیقی همتوان است چرا که هر نقطه روی دایره را که به مرکز دایره وصل کنید و آن را امتداد دهید خط اعداد حقیقی را در نقطه ای منحصربه فرد قطع می کند. پس بازه مورد نظر با اعداد حقیقی همتوان است.