ШЁЩҮ ЩҶШ§Щ… Ш®ШҜШ§
ШЁШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ Ш§ШҙЪ©Ш§Щ„ ЩҮЩҶШҜШіЫҢ Щ…Ш§ЩҶЩҶШҜ Щ…ШіШӘШ·ЫҢЩ„ ШЁЩҮвҖҢШұШ§ШӯШӘЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш§ЫҢЩҶ Щ…ЩҲШ¶ЩҲШ№ ШұШ§ Ш§Ш«ШЁШ§ШӘ Ъ©ШұШҜ.
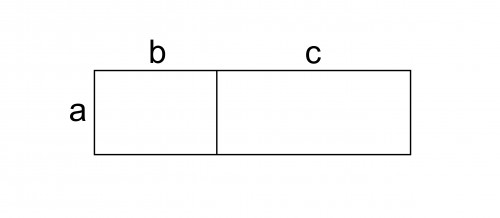
Ш№ШұШ¶ ЩҮШұ ШҜЩҲ Щ…ШіШӘШ·ЫҢЩ„ ШЁШұШ§ШЁШұ ШЁШ§ $a$ Ш§ШіШӘШҢ ЩҲЩ„ЫҢ Ш·ЩҲЩ„ Щ…ШіШӘШ·ЫҢЩ„ Ъ©ЩҲЪҶЪ©ШӘШұ ШЁШұШ§ШЁШұ ШЁШ§ $b$ ЩҲ Ш·ЩҲЩ„ Щ…ШіШӘШ·ЫҢЩ„ ШЁШІШұЪҜШӘШұ ШЁШұШ§ШЁШұ ШЁШ§ $c$ Ш§ШіШӘ.
Ш§ЪҜШұ Ш¬Щ…Ш№Ш§ЩӢ Щ…ШіШ§ШӯШӘ ЩҮШұ ШҜЩҲ Щ…ШіШӘШ·ЫҢЩ„ ШұШ§ ШЁШ§ $S$ ЩҶЩ…Ш§ЫҢШҙвҖҢШҜЩҮЫҢЩ…ШҢ ШЁШ§ Ъ©Щ…ЫҢ ШҜЩӮШӘ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҒЩҮЩ…ЫҢШҜ Ъ©ЩҮ:
$$S=ab+ac$$
Ш§Щ…Ш§ Ш§ЪҜШұ ЩҮШұ ШҜЩҲ Щ…ШіШӘШ·ЫҢЩ„ ШұШ§ ЫҢЪ© Щ…ШіШӘШ·ЫҢЩ„ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢЩ…ШҢ ШҜШұ Ш§ЫҢЩҶвҖҢШөЩҲШұШӘ Ш·ЩҲЩ„ ШЁШұШ§ШЁШұ ШЁШ§ $b+c$ Щ…ЫҢвҖҢШҙЩҲШҜ. ЩҫШі:
$$S=a(b+c)$$
ЩҲ ШҜШұ ЩҶЩҮШ§ЫҢШӘ:
$$\left.\begin{array}{l}
S=ab+ac\\ S=a(b+c)
\end{array}\right\rbrace\Longrightarrow a(b+c)=ab+ac$$