اگر زاویه ها را $A $ و $ B $ و $C $ بنامیم داریم:
$$ \frac{A}{6} = \frac{C}{5} = \frac{B}{1} = \frac{A+B+C}{12} =15$$
پس داریم:$A=90 $ و $C=75 $ و $B=15 $
کوچکترین ارتفاع همان ارتفاع وارد بر وتر است بزرگترین ضلع هم وتر است.
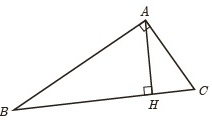
$S= \frac{AH \times BC}{2}= \frac{AB \times AC}{2} $ پس $ AH \times BC=AB \times AC$
به کمک زاویه $ B $ داریم:
$$ sin(15)= \frac{AC}{BC} \Rightarrow AC=sin(15) \times BC $$
و
$$ cos(15)= \frac{AB}{BC} \Rightarrow AB=cos(15) \times BC $$
با جایگذاری این دو رابطه داریم:
$ AH \times BC=AB \times AC=sin(15) \times BC \times cos(15) \times BC$
پس
$ \frac{AH}{BC} =sin(15) \times cos(15)= \frac{2sin(15) \times cos(15)}{2}= \frac{sin(30)}{2}= \frac{1}{4} $