یک راه برای پیدا کردن مسیر مناسب این است که ابتدا نمودار تابع را رسم کنید یعنی شکل سهبعدی حاصل از $z=f(x,y)$. با همان نرمافزار Mathematica که شما از نسخهٔ برخطش در پیوند گذاشتهشده در متن پرسشتان برای حد استفاده کردهاید این کشیدن با دستور زیر انجام میشود.
Plot3D[(y*x^2)/(x^2+y^3),{x,-1,1},{y,-1,1}]
شکل حاصل در زیر آوردهشدهاست.
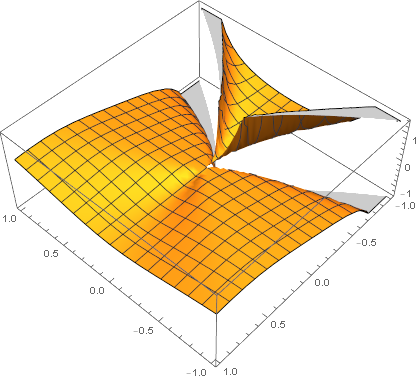
با دوران شکل به گونهای که عمود به صفحهٔ $x\circ y$ به آن نگاه کنیم شکل زیر را دارید.
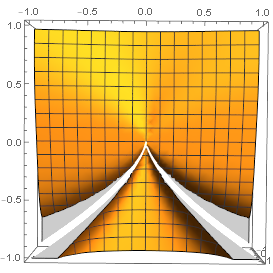
همان گونه که متوجه شدهاید یک خم هشتی-شکل نوکتیز دارید که از بالای این خم به آن نزدیک شدن به منفیبینهایت میروید و با نزدیک شدن به آن از زیر به مثبت بینهایت. این خم زیر محور $x$ها قرار دارد و نوک تیزش در $(0,0)$ قرار دارد. این تابع نه تنها در این نقطه بلکه در امتداد کل این خم هشتی-شکل حد ندارد. برای اینکه این مشکل را ببینید، قرار دهید $x=0.001$ و سپس مقدار $y$ را عددی کوچک ولی منفی دهید و آن را تغییر دهید، برای هر مقداری که بردارید معمولا عدد کوچک میگیرید مثلا $0.01$ ولی وقتی نزدیک به مقدار $0.01$ میشوید به عددی مثل $47223700000000$ میرسید!
برای اینکه بتوانیدخم مورد نظر را با روشهای تقریب عددی با ضابطهای تقریب بزنید نیاز دارید چند نقطهٔ تقریبا روی یا نزدیک به آن را پیدا کنید و سپس یک درونیابی یا روش دلخواه دیگری استفاده کنید. با افزایش دامنه و برد رسم نمودار سهبعدی بالا و نگاه کردن عمود میتوانید چند نقطه انتخاب کنید و حسی در مورد شکل خم پیدا کنید.
Plot3D[(y*x^2)/(x^2+y^3),{x,-10,10},{y,-10,10},PlotRange->{{-10,10},{-10,10},{-1000,1000}}]
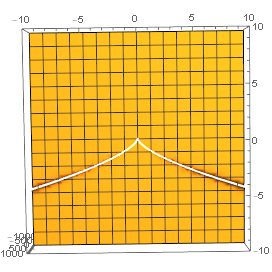
اما آیا میشود بدون تقریب زدن مسیر دقیق را پیدا کرد؟ بلی. توجه کنید که چه زمانی یک کسر که صورت آن برای هر متغیر متناهیِ ورودی عددی متناهی میشود تعریفنشده شود (به بینهایت برود)؟ زمانی که مخرج کسر صفر شود. پس برای بدست آوردن این خم هشتی کافیست $x^2+y^3=0$ را حل کنیم. بیاییم از یک ترفند برای پارامتریکردنش استفاده کنیم. از $x^2+y^3=0$ داریم که $x^2=-y^3$ اکنون این دو مقدار برابر را با پارامتر جدیدی نشان دهید مانند $t$. این پارامتر فقط مقدارهای مثبت میگیرد چون با $x^2$ برابر است. این نتیجه میدهد که $y^3$ و در نتیجه خود $y$ منفی است. پس حتی اگر شکل را هم نمیدیدیم میتوانستیم با این محاسبه بدانیم که این خم در زیر محور $x$ها قرار دارد. به هر حال خیلی ساده از $x^2=-y^3=t$ داریم $x=\pm\sqrt{t}$ و $y=\sqrt[3]{t}$. خم هشتیمان کاملا رو شد.
$$c=\lbrace (-\sqrt{t},-\sqrt[3]{t})\mid t>0\rbrace\cup\lbrace (\sqrt{t},-\sqrt[3]{t})\mid t > 0\rbrace$$
اکنون نشان میدهیم که نه تنها در صفر بلکه بر روی کل این خم، تابع شما حد ندارد. یک نقطهٔ دلخواه مانند $(x_0,y_0)$ بر روی خم $c$ به شکل $(\sqrt{t},\sqrt[3]{t})$ به ازای یک $t_0$ نوشته میشود. یا با طول منفی که بدون کاستن از کلیت ما برای طول مثبت را انجام میدهیم که برای حالت $y < -\sqrt[3]{t_0}$ هیچ چیز متفاوت اضافهتری پیش نمیآید پس همین اثبات برای آن هم برقرار میشود. همانطور که در قبلا گفته شد، یک بار از بالای خم و یک بار از پائین خم به سمت این نقطه حرکت میکنیم. روی خط عمودی $x=\sqrt{t_0}$ حرکت کنید وقتی $y > -\sqrt[3]{t_0}$ است داریم $x^2+y^3 > 0$ پس چون صورت کسر که برابر ضرب توان دوی طول در توان یک عرض نقطهها میشود منفی است، کل کسر منفی است. چون مخرج به صفر نزدیک و نزدیکتر میشود پس کل کسر به منفی بینهایت میل میکند. اکنون از زیر خم روی هم خط عمودی حرکت کنید. چون $y < -\sqrt[3]{t_0}$ است پس $x^2+y^3 < 0$ و در نتیجه کل کسر مثبت میشود. بنابراین از این سمت به مثبت بینهایت میل میکند. چون $t_0$ دلخواه بود پس ثابت کردیم که برای هر نقطهٔ دلخواه از این خم، از بالا که به آن نزدیک میشویم، تابع به $+\infty$ نزدیک میشود و از پائین که به آن نزدیک میشویم، تابع به $-\infty$ نزدیک میشود. اکنون برای پرسش شما که فقط مبدأ را خواستهاست کافی است قرار دهید $t=0$.