المپیاد ریاضی دانش آموزی $92$(سی و دومین دوره) سوال $3$

Question

در مثلث $ABC$ نقطه $D$ روی ضلع $BC$ به گونه ای قرار گرفته که زاویه های $\widehat{BAD}$ و $\widehat{CAD}$ و $\widehat{ABC}$ باهم برابرند و طول پاره خط های $BD$ و $DC$ به ترتیب برابر 1 و 2 است. طول $AB$ چقدر است؟

1) $\sqrt{2}$

2) $\sqrt{3}$

3) $\frac{\sqrt{6} }{2}$

4) $\frac{\sqrt{3} }{2}$

5) $\frac{\sqrt{6} }{3}$

Answer 1

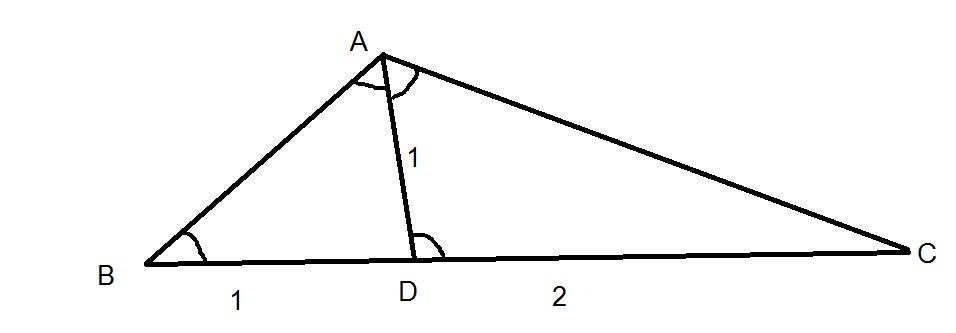
جواب میشه $\frac{ \sqrt{6} }{2}$ . زیرا با توجه به شکل زیر، با توجه به قانون کسینوس و قضیه ای از هندسه " در هر مثلث، نیمساز زاویه داخلی، ضلع روبرو به آنرا به نسبت دو ضلع زاویه قطع میکند" یعنی: $\frac{AB}{AC}= \frac{BD}{DC}$ . لذا نتیجه میشود $AB= \frac{1}{2}AC$.

با توجه به قضیه کسینوسها در مثلث $ABD$ داریم:

$AB^{2} = 2(1+\cos A)$.

از طرفی در مثلث $ADC$ با توجه به قانون کسینوسها داریم:

$AC^{2}=5-4\cos A$.

لذا باتوجه به اینکه $AB= \frac{1}{2}AC$ , و حل معادله ی حاصل از آن یعنی

$8+8\cos A=5 - 4\cos A$

داریم $\cos A= \frac{-1}{4}$

و با جایگذاری آن در معادله اول به دست می اید $AB= \frac{ \sqrt{6} }{2}$ .

Answer 2

اگر در مثلث $ABC$ نیمساز راس $A$ که آن را $AD$ مینامیم رسم کنیم دو رابطه ی زیر همواره برقرار هستند(هندسه 2)

$$\frac{AB}{AC} = \frac{BD}{DC}$$ $$(AD)^{2} =AB.AC-BD.DC$$

حال چون در این سوال دو زاویه از مثلث کوچک $ABD$ طبق فرض سوال برابرند لذا این مثلث متساوی الساقین است یعنی $AD=BD=1$ پس با جایگذاری مقادیر داده شده در دو رابطه بالا داریم:

$\frac{AB}{AC} = \frac{1}{2}$ لذا $2AB=AC$

$(1)^{2} =AB.AC-1 \times 2$ لذا $3=AB.AC$

پس با جایگذاری $2AB=AC$ در رابطه بدست آمده داریم :

$3=AB.(2AB) \Rightarrow \frac{6}{4} =\frac{3}{2} = (AB)^{2}$

یعنی

$AB= \frac{ \sqrt{6} }{2}$

Answer 3

راه حل هایی که توسط دو عزیز در بالا داده شده است بسیار خوب است ولی راه ساده ی دیگری نیز وجود دارد ،که به این شرح است: نیمساز زاویه Dرا رسم می کنیم و محل برخورد آنرا با AC، را با حرف K نمایش میدهیم،بوضوح پیداست که نیمسازی که کشیدیم با خط AB موازی است ،طبق قضیه نیمساز ها ،نیمسازی که از زاویه Dرسم شد ضلع ACرا به نسبت 1 و2 تقسیم می کند ،طبق تالس(DK =$\frac{2AB}{3}$(AB , و از طرف دیگر از تشابه دو مثلثADK وABD می توانیم DK را بدست آوریم که برابر با $\frac{1}{AB}$ میشود ،با حل یک معادله ی ساده به جواب میرسیم.