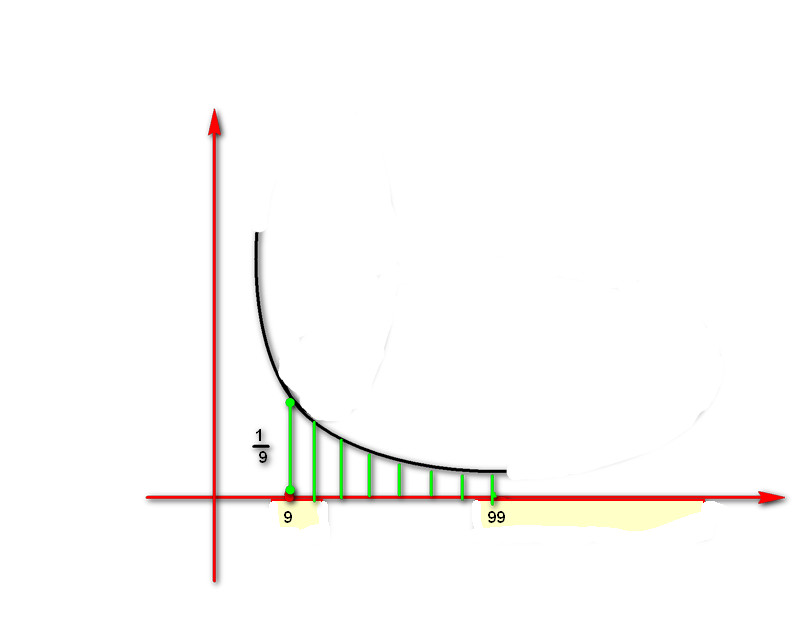
 اگر تابع$ y= \frac{1}{x} $ رارسم کنیم طبق شکل رسم شده شده مجموع پاره خط های سبز رنگ جواب مسئله خواهد بود.دراین شکل اعداد از 9 تا 99تصویر را به 90 شکل تقریبآذوزنقه ای به ارتفاع یک واحدتقسیم می کند.هردو ذوزنقه در یک ضلع مشترک است مجموع مساحت ذوزنقه ها را به دو روش محاسبه میکنیم.
اگر تابع$ y= \frac{1}{x} $ رارسم کنیم طبق شکل رسم شده شده مجموع پاره خط های سبز رنگ جواب مسئله خواهد بود.دراین شکل اعداد از 9 تا 99تصویر را به 90 شکل تقریبآذوزنقه ای به ارتفاع یک واحدتقسیم می کند.هردو ذوزنقه در یک ضلع مشترک است مجموع مساحت ذوزنقه ها را به دو روش محاسبه میکنیم.
$s= \frac{ \frac{1}{9} + \frac{1}{10} }{2}+ \frac{ \frac{1}{10} + \frac{1}{11} }{2}...+ \frac{ \frac{1}{98} + \frac{1}{99} }{2} $
حال مساحت ذوزنقه ها را به روش انتگرال بدست می آوریم.
$s= \int_a^b \frac{1}{x}dx $را محاسبه می کنیم یعنی $=lnx =ln99-ln9=ln \frac{99}{9} =ln11=2.3978$s
بنابراین
$s= \frac{ \frac{1}{9} + \frac{1}{10} }{2}+ \frac{ \frac{1}{10} + \frac{1}{11} }{2}...+ \frac{ \frac{1}{98} + \frac{1}{99} }{2}=2.3978 $
اگر این معادله را حل کنیم
$ \ \frac{1}{9} + \frac{1}{10} + \frac{1}{10} + \frac{1}{11}+ \frac{1}{11}+ ...+ \frac{1}{98} + \frac{1}{98} + \frac{1}{99}=4.7956 $
و مجموع معکوس های عددهای 9 تا 99 را A فرض کنیم وبا توجه به اینکه مجموع معکوس های اعداد 10 تا 98 دوبار تکرار شده است خواهیم داشت $A+A- \frac{1}{9}- \frac{1}{99}=4.7956 $ در نتیجه
2A=4.9168 ومقدار تقریبی A=2/4584$ $بدست میآید.این مقدار با مقدار واقعی 0.001 تفاوت داردوآن بدلیل آن است که ذوزنقه ها در قسمت بالای آنها انحنا دارداگر به جای آنکه از معکوس عدد 9 ازمعکوس عدد 99 شروع و به معکوس عدد 999 ختم کنیم انحنا خیلی کمتر و به عدد واقعی از همین روش می رسیم پایان.