Question

ثابت کنید«مجذور ارتفاع وارد بر وتر برابراست با ضرب دوپاره خط بدست امده»

یعنی AD^2 = BD*CD

Answer 1

راهنمایی: قضیه فیثاغورث را برای سه مثلا قائم الزاویه به کار ببرید.

$$AB^2=AD^2+BD^2\\ AC^2AD^2+CD^2\\ BC^2=AB^2+AC^2$$

حال از $BC=BD+CD$ ، اتحاد مربع دوجمله ای و روابط بالا استفاده کنید.

Comments

سلام
ممنونم از پاسختون

Answer 2

مثلث قائم الزاویه زیر را با زاویه قائمه A و ارتفاع AH در نظر بگیرید:

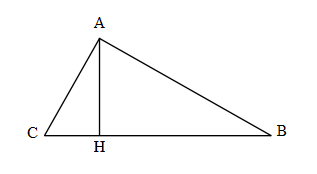
بنا بر قضیه تشابه دو مثلث AHC با AHB متشابه هستند چون هر دو با مثلث اصلی ABC متشابه هستند پس زوایای این مثلث ها با زوایای مثلث اصلی برابر هستند. بنابر این چون زاویه HAC با ABH برابر است در شکل زیر BD را به اندازه AH و BC را به اندازه AC در نظر میگیرم و از C به D وصل میکنم:

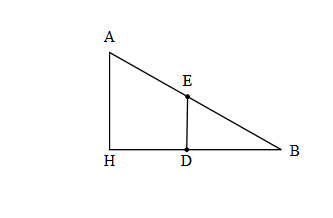
مثلث EBD یا AHC به حالت ض ز ض برابر است از طرفی ED با AH موازی است چون ED بر DB عمود است و AH بر HB عمود است.

بنا بر قضیه اثبات شده تالس می دانیم: BD/BH = ED/AH

حال BD را با AH و ED را با CH جایگزین می کنیم:

AH/BH = CH/AH

بنابر این طرفین را در هم و وسطین را در هم ضرب می کنیم و داریم:

AH^2 = BH*CH