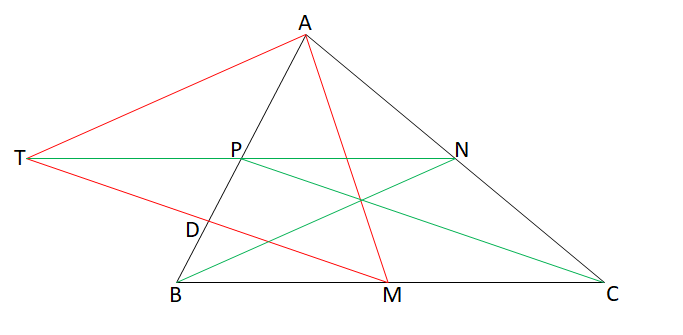
در مثلث ABC وسط اضلاع AB , BC , CA را به ترتیب P , M , N بنامید. از M خطی به موازات CP رسم میکنیم تا امتداد NP را در T قطع کند. چون PT موازی MC است و PC نیز موازی MT است پس چهارضلعی PCMT متوازی الاضلاع است و بنابراین (1) PC=MT.
از طرفی چون PCMT متوازی الاضلاع است پس PT=MC=BC/2=NP و همچنین AP=BP و در نتیجه به دلیل اینکه در چهارضلعی ANBT قطر ها همدیگر را نصف میکنند پس این چهارضلعی متوازی الاضلاع است و در نتیجه (2) AT=NB.
ار (1) و (2) به این نتیجه میرسیم که اضلاع مثلث AMT برابر با میانه های مثلث است و بنابراین با میانه ها توانستیم مثلث بسازیم. حکم اول ثابت شد.
حال میدانیم PT=MC=MB و PT موازی MB است. بنابراین مساحت مثلث TPD برابر با مساحت مثلث DMB است و یعنی جمع مساحت مثلث های TPD و ADM برابر جمع مساحت مثلث های ADM و DMB است که همان مساحت مثلث ABM است که نصف مساحت کل است. پس تا کنون داریم:
$$ S_{TPD} + S_{ADM} = S_{ABM} $$
حال توجه کنید به دلیل اینکه چهارضلعی ANBT متوازی الاضلاع است، مساحت مثلث های APT و PNB با هم برابر است.
یعنی در کل:
$$ S_{ATM} = S_{APT} + S_{ADM} + S_{TDP} = S_{PNB} + S_{ABM} = \frac{1}{4}S_{ABC} + \frac{1}{2} S_{ABC} = \frac{3}{4} S_{ABC} $$
پس حکم دوم هم ثابت شد.