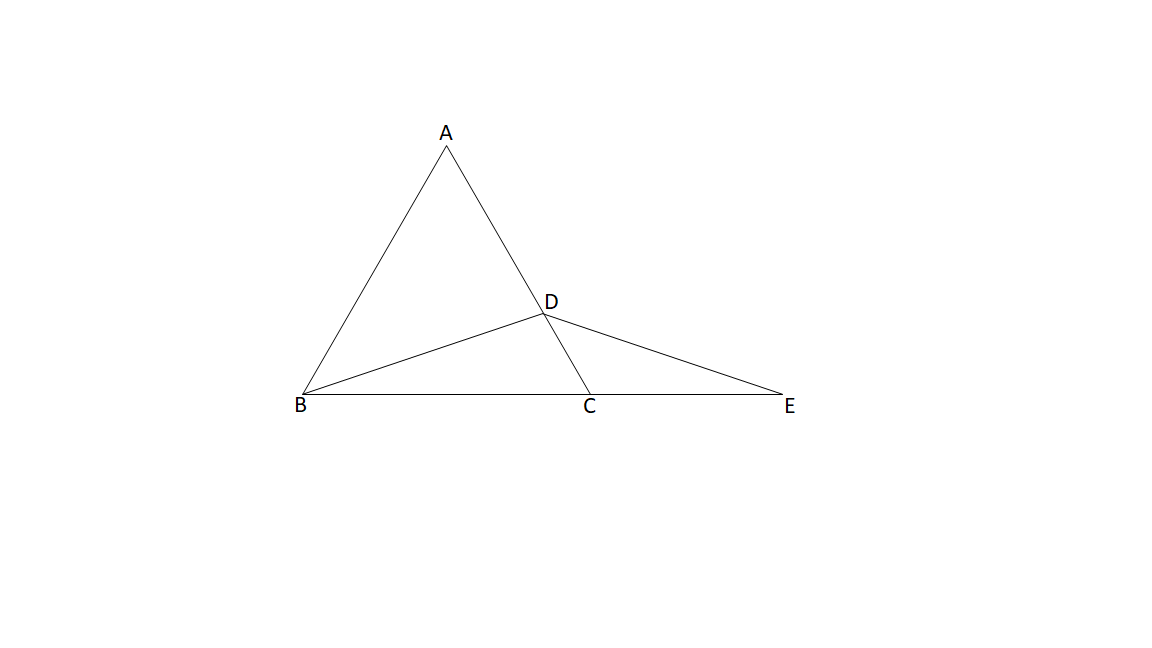
با نوشتن قضیه ی سینوس ها در مثلث $CDE$ داریم:
$$ \frac{DE}{sin( \widehat{DCE})} = \frac{CE}{sin( \widehat{CDE} )} $$
و با نوشتن قضیه ی سینوس ها در مثلث $ABD$ داریم:
$$ \frac{BD}{sin( \widehat{BAD} )} = \frac{AD}{sin( \widehat{ABD} )} $$
با تقسیم طرفین این دو تساوی داریم:
$$ \frac{DE}{BD} . \frac{sin( \widehat{BAD})}{sin( \widehat{DCE})} = \frac{CE}{AD} . \frac{sin( \widehat{ABD)}}{sin( \widehat{CDE} )} $$
که سمت چپ این تساوی برابر یک است( چراکه $DE=BD$ و همچنین چون $ \widehat{BAD} =60 , \widehat{DCE} =120$ بنابراین $sin( \widehat{DCE})=sin(\widehat{BAD} )$ ) . پس:
$$\frac{CE}{AD} = \frac{sin( \widehat{CDE} )}{sin( \widehat{ABD} )} (1) $$
حال داریم:
$$ \widehat{CDE} =180- \widehat{DCE} - \widehat{CED} $$
$$=60- \widehat{DEC} $$
و همچنین:
$$ \widehat{ABD} = \widehat{ABC} - \widehat{DBC} $$
$$=60- \widehat{DBC} =60- \widehat{DEC} $$
پس زوایای $ \widehat{CDE} $ و $ \widehat{ABD} $ با هم برابرند و بنابراین طبق $(1)$ داریم: $AD=CE$