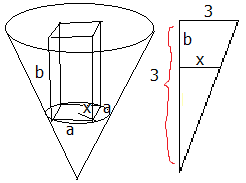
$$\frac{3-b}{3}=\frac{\frac{a\sqrt{2}}{2}}{3}\Longrightarrow 3-b=\frac{a}{\sqrt{2}}\Longrightarrow b=3-\frac{a}{\sqrt{2}}$$
مساحتِ مکعبمستطیل را با $v$ نمایش دهید.
$$v=(3-\frac{a}{\sqrt{2}})a^2=3a^2-\frac{a^3}{\sqrt{2}}$$
نسبت به $a$ مشتق بگیرید.
$$v'_a=6a-\frac{3a^2}{\sqrt{2}}$$
ریشههای مشتق را بیابید.
$$a=0\text{ or }a=\frac{6}{\frac{3}{\sqrt{2}}}=2\sqrt{2}$$
پس $a=2\sqrt{2}$ و $b=3-\frac{2\sqrt{2}}{\sqrt{2}}=1$ و در نتیجه حجم خواستهشده برابر است با $1(2\sqrt{2})^2=8$.