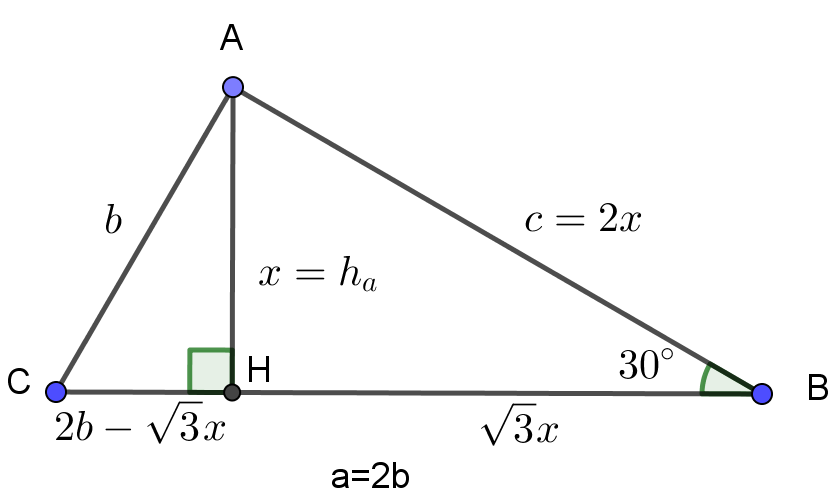
درمثلث قائم الزاویه AHC:
$ (2b- \sqrt[]{3}x) ^{2}=b^{2}-x^{2} $
پس ازمرتب کردن $ 4x^{2}-4\sqrt[]{3}bx+3b^{2} =0$ لذا
$(2x- \sqrt[]{3}b) ^{2}=0$ درنتیجه $ \frac{x}{b}=\frac{\sqrt[]{3}}{2} $
پس زاویه $C= 60^{ \circ } $ و زاویه $ A=90^{ \circ } $
راه حل دوم:
$ \frac{ h_a \times 2b }{2}= \frac{1}{2}b \times 2h_a sin \hat{A} $
درنتیجه: $sin \hat{A}=1$ پس $\hat{A}=90^{ \circ } $