فکر کنم شما تفاوت بین free resolution و minimal free resolution را بخواهید که تحلیل آزاد و تحلیل آزاد کمینه ترجمه میشوند. ولی شیوهای که پرسش را پرسیدهاید کمی شک میسازد. اینکه ویرگول را بین تحلیل آزاد و کمینه گذاشتهاید ممکن است این فکر را به ذهن خواننده بیاورد که تأکید دارید «تحلیل آزاد کمینه» منظورتان نیست و کمینهبودن درازا (طول) تحلیل آزادتان منظور است.
هر تحلیل آزاد کمینه یک تحلیل آزاد نیز است ولی عکس آن برقرار نیست. تحلیل آزاد کمینه یک تحلیل آزاد است که مدولهای آزاد تحلیلتان را از کمترین رتبهٔ ممکن گرفتهباشید که در حد یکریختی یک تحلیل یکتا میباشد. برای نمونه ایدهآل $I$ از حلقهٔ $R$ که در زیر آوردهشدهاست را به عنوان یک $R$-مدول در نظر بگیرید. در زیر یک تحلیل آزاد از آن آوردهشدهاست. چون کوچکترین مجموعه از نظر عدد اصلی cardinal که $I$ را به عنوان $R$-مدول تولید کند دو عضوی است مانند $\{x,y\}$ پس $R^2$ از نظر رتبه کمینه است. در واقع کمینه رتبهای که برای مدول آزاد یکم میتوانیم برداریم برابر با کمینه تعداد عنصری است که برای تولید مدولمان نیاز داریم و سپس برای مدولهای آزاد پسین، کمینه تعداد عنصری که برای تولید هستههای همریختیهای گامهای تحلیلمان نیاز داریم میشوند. همانگونه که مشخص است برای هستهٔ یکم، یک عنصر کافیاست و سپس هستهٔ دوم به بعد صفر میشوند. پس این تحلیل آزاد، تحلیل آزاد کمینه نیز است.
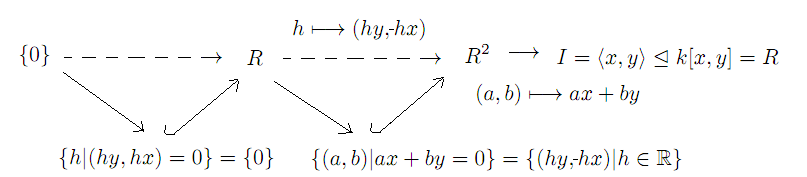اما آیا میتوان نمونهای آورد که تحلیل آزاد باشد ولی تحلیل آزاد کمینه نباشد؟ بلی به سادگی. از نمونهٔ بالا میتوانید ایده بگیرید. میدانید که برای یک ایدهآل میتوانید مولدهای گوناگونی بردارید که الزاما همگی همعدداصلی نیستند. اگر برای ایدهآلتان یک مولد با تعداد ناکمینه عنصر برمیداشتید و نگاشت نخست را مشابه بالا ولی متناظر با مولد ناکمینهتان برمیداشتید آنگاه چون رتبهٔ مدول آزاد نخستتان کمینه نبود، به طبع تحلیلتان نیز تحلیل آزاد کمینه نیز نمیگشت. این تعداد عنصرهای مولد کمینه که رتبههای مدولهای آزاد در تحلیل آزاد کمینهتان نیز هستند، عددهای مهمی هستند و آنها را عددهای بتی نیز صدا میکنند.
