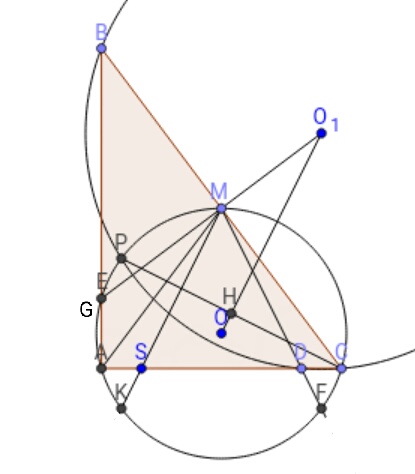
$O_{1}$ :مرکز دایره محیطی مثلث $BCD$
$O$ :مرکز دایره محیطی مثلث $AMC$
$E$: محل تقاطع دوم خط $O_{1}M$ و دایره $O$
$G$: محل تقاطع خط $AB$ و دایره $O$ بین $A$ و $B$
$F$: محل تقاطع دوم خط $MD$ و دایره $O$
$H$: محل تقاطع خط $PC$ و خط $O_{1}O$
$S$: روی $AC$ طوری انتخاب میکنیم تا $AS=DC$
$K$: محل تقاطع دوم خط $MS$ و دایره $O$
برای سادگی کار تمام زوایا و کمانها را با $x$ و$y$ و$z$ نام گذاری و اندازه میگیریم.
$C$ را به $P$ وصل میکنیم و قرار میدهیم:
$$ \hat{PCM} =y \Rightarrow \frown PM=2y$$
$$ \hat{PCA}=x \Rightarrow \frown AP=2x$$
$$ \Rightarrow \frown AM=2x+2y= \frown CM$$
چون مثلث $AMC$ متساوی الساقین است، پس:
$$ \hat{MAC} =x+y \Rightarrow \frown CM=2x+2y$$
چون دو مثلث $MSA$ و $MDC$ با (ض.ض.ض) هم نهشتند، پس:
$$ \hat{AMK}=\hat{FAC}=z$$
$$ \Rightarrow \frown AK=2z \frown FC$$
چون مثلث $AMD$ متساوی الساقین است در نتیجه:
$$ \hat{SMD}=x+y \Rightarrow \frown KF=2x+2y$$
چون $PC$ وتر مشترک دو دایره می باشند پس $O_{1}O$ عمود منصف $PC$ می باشد و $H$ قائمه هست.
محل تقاطع $O_{1}O$ و $MC$ را $Q$ مینامیم و چون $BC$ وتر دایره $O_{1}$ می باشد و $O_{1}M$ آن را به دو قسمت مساوی تقسیم میکند پس بر هم عمودند.
در نتیجه در دو مثلث $QHC$ و $QMO_{1}$ دو زاویه برابرند، داریم:
$$(*) \hat{MO_{1}Q}=y$$
از مفروضات داریم:
$$3(2x+2y)+2(2z)=360$$
$$ \Rightarrow \frac{3x+3y}{2} +z=90$$
حال $B$ را بدست میآوریم:
$$B=90-(x+y)= \frac{x+y}{2} +z$$
کمان $GM$ را محاسبه میکنیم:
$$B= \frac{ \frown AC- \frown GM}{2} $$
$$ \Rightarrow \frown GM=x+y+2z=2B$$
کمان $EM$ را محاسبه میکنیم :
مماسی بر دایره $O$ در نقطه $M$ رسم میکنیم و چون $BME$ قائمه است و مماس با $AC$ موازی است پس زاویه بین مماس و $ME$ برابر $B$ میباشد. پس:
$$ \frown EM=2B= \frown GM$$
درنتیجه $G$ و $E$ بر هم منطبق هستند و مکان $E=G$
چون$DC$ وتر دایره $O_{1}$ می باشد پس عمود منصف آن از مر کز $O_{1}$ میگذرد.
و چون مثلث $DFC$ متساوی الساقین است پس عمود منصف $DC$، نیمساز $DFC$ میباشد درنتیجه چون $DFC=x+y$ در نتیجه خط $O_{1}F$ کمان $MC$ را به دو قسمت مساوی به اندازه $x+y$ تقسیم میکند و محل برخورد کمان و خط را $N$ مینامیم.
چون
$$x+y+2z= \frown NF= \frown EM$$
در نتیجه دو وتر $FN=PM$ که در خارج دایره $O$ همدیگر را در $O_{1}$ قطع میکنن مثلث متساوی الساقین $EO_{1}F$ را میسازند و $O_{1}O$ نیمساز $EO_{1}F$ و از (*) و
$$ \hat{FO_{1}E}=x+y $$
داریم:
$$OO_{1}E=\frac{x+y}{2}=y$$
$$ \Rightarrow x=y$$
درنتیجه $PC$ نیمساز زاویه $ACB$ میباشد.