شعاع دایره محیطی هر مثلث برابر است با $R= \frac{abc}{4S} $درنتیجه داریم $S= \frac{abc}{4R} $حال اگر بجای اضلاع مثلث از فرمول $ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}=2R $استفاده کنیم
$S= \frac{2RsinA.2RsinB.2RsinC}{4R} = \frac{2 R^{2}sinA.sinB.sinC }{1} =2 R^{2} sinAsinBsinC$بدست می آید.
برای اثبات قضایا مسئله بالا از شکل زیر استفاده می کنیم
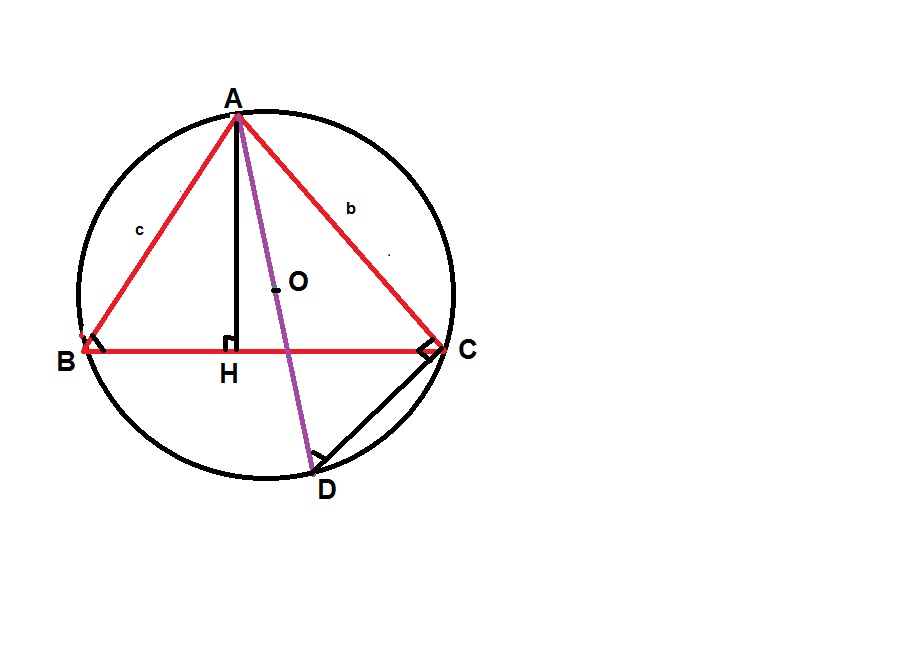
AD قطر دایره محیطی مثلث است ومثلث های ABH وADC همنهشت هستند(به حالت دو زاویه مساوی)
اگر نسبت همنهشتی را بنویسیم داریم:$ \frac{AH}{b} = \frac{c}{2R} $اگر دراین تناسب به جای AH که ارتفاع مثلث ABC میباشد مقدار $ \frac{2S}{a} $ قرار دهیم($ُS= \frac{a.AH}{2} $) خواهیم داشت $ \ \frac{ \frac{2S}{a} }{b} = \frac{c}{2R} $ درنتیجه 4RS=abc و$R= \frac{abc}{4S} $
وبرای سینوس ها میتوانیم از طریق مساحت مثلث یا بکمک شکل اثبات کنیم مساحت مثلث ABCبرابراست با
$ \frac{a h_{a} }{2} = \frac{b h_{b} }{2} = \frac{c h_{c} }{2} $ درنتیجه داریم مثلاAH=csinB=$ h_{a} $
یعنی acsinB=basinC=cbsinA هرگاه جفت -جفت این تساویها راساده کنیم داریم$ \frac{b}{sinB} = \frac{c}{sinC} = \frac{a}{sinA} $ واما چرا این نسبت ها برابر 2R است ؟ باتوجه به شکل$ \frac{c}{2R} = \frac{AH}{b} $اگر به جای AH مقدار CsinB قرار دهیم ومقداردو کسر را به c ساده کنیم خواهیم داشت $ \frac{b}{sinB} =2R$ وبرای نسبت های دیگر نیز به همین ترتیب بدست میآید.