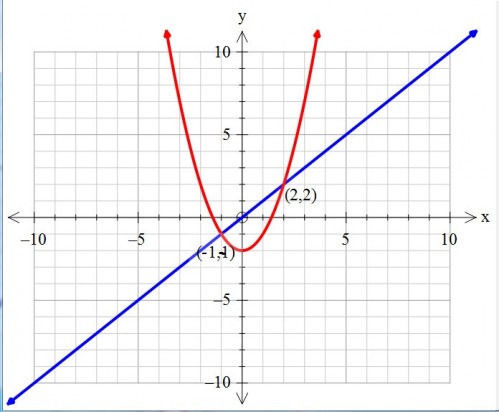
بنام خدا.ابتدانقاط تقاطع دو نمودار رابدست می آوریم $ x^2-2=x \Rightarrow x^2-x-2=0 \Rightarrow (x-2)(x+1)=0 $ بنابراین نقاط تقاطع
(1-,1-) و (2,2) خواهد بود طبق شکل نمودار y=x در بازه ی (2و1-)بالای نمودار $y=x^2-2 $ درنتیجه داریم
حدود انتگرال از1- تا2 میباشد.
$s= \int xdx- \int_{-1}^2 (x^2-2)dx=\frac{x^2}{2}-( \frac{x^3}{3}-2x)=( \frac{4}{2} - \frac{1}{2})-(( \frac{8}{3}-4)- (\frac{-1}{3}+2))= \frac{3}{2}-( \frac{-4}{3}- \frac{5}{3} ) $
$ \Rightarrow s= \frac{3}{2} +3= \frac{9}{2} $