در شکل زیر :
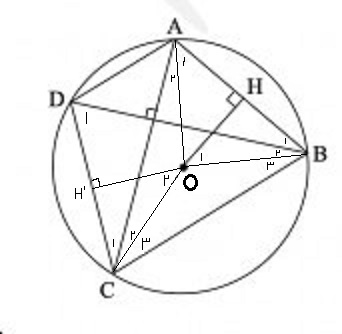
داریم: (در ادامه نام زاویه ها آورده شده)
$$
\hspace{-2cm}
\begin{align*}
&A_2=C_2 \Rightarrow A_2-C_2=0\\&A_1+A_2=D_1 \Rightarrow A_1+A_2=90-C_1\\&A_1=B_1+B_2 \Rightarrow A_1+A_2-C_2=B_1+B_2 \Rightarrow 90-C_1-C_2=B_1+B_2 \\&\Rightarrow O_2=B_1+B_2
\end{align*}
$$
پس به دلیل وتر و یک زاویه مثلث های $OHB$ و $CH'O$ با هم همنهشت اند. پس $OH=H'C=\frac{1}{2}DC$.