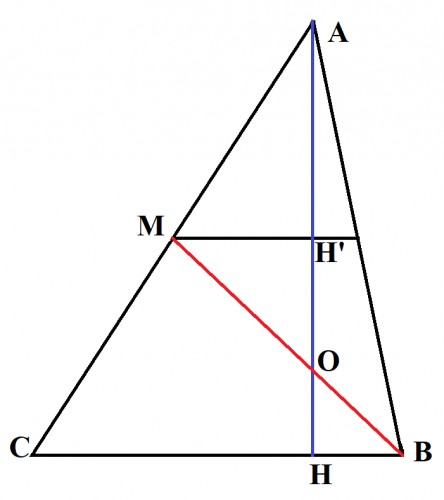
ارتفاع AH برابر میانه BM است. از نقطه M پاره خطی به موازات قاعده می کشیم. بنابر قضیه تالس $$AH'=H'H=\frac{1}{2}AH$$
دو مثلث OHB و OH'M با هم متشابهند. پس داریم:
$$ \frac{OH'}{OH} = \frac{OM}{OB} $$
صورت و مخرج را با هم جمع می کنیم:
$$ \frac{HH'}{OH} = \frac{BM}{OB}= \frac{AH}{OB} $$
از آنجایی که $AH$ دو برابر $H'H$ است. پس $OB$ دو برابر $OH$ است. از طرفی:
$$ Sin(\angle OBH) = \frac{OH}{OB}= \frac{1}{2} $$
پس زاویه $OBH$ برابر $30^\circ$ است.