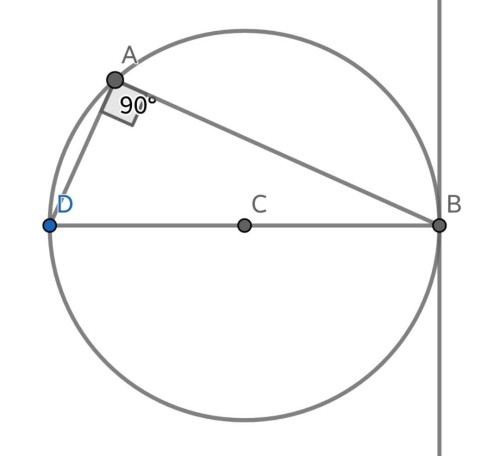
مطالق شکل بالا، با فرض معلوم بودن اندازه پاره خط $AB$ ، خطی گذرنده از نقاط $B,C$ را رسم میکنیم و تقاطع خط با دایره را D می نامیم. واضح است که اندازه زاویه $ \hat{A} $ برابر ۹۰ درجه است. $ \alpha = \hat{ABC} $ در نظر میگیریم. پس:
$$ cos( \alpha )= \frac{AB}{BD}= \frac{AB}{2r} $$
اندازه زاویه خواسته شده برابر با $90- \alpha $ است، به عبارتی دیگر:
$$ 90- \alpha=90- arccos(\frac{AB}{2r})$$