ببینید، اینطور نیست که ابتدا عدد $\pi$ را تعریف کردهباشند و سپس رفته باشند مساحت دایره را بر حسب این عدد بدست بیاورند! ابتدا روی محیط و مساحت دایره کار کردهاند و دیدهاند که محیط و مساحت دایره نسبت به قطر و مجذور شعاع یک نسبت ثابت دارند. پس یک عدد داریم. اسم آن را $\pi$ گذاشتند. سپس به محاسبه و بهدست آوردن این عدد اقدام کردند. جملهٔ اینکه سالها از عدد $\pi$ استفاده شده ولی رابطهٔ این عدد با مساحت دایره ملموس نبودهاست، جملهٔ نادرستی است. اینکه برای فردی چیزی ناملموس باشد نتیجه بر ناملموس بودن آن برای همه را نمیدهد. این نوع نتیجهگیری از نوع استقرای ناریاضی و حتی بیشتر، استقرای ناریاضی با مشاهدهٔ کم است.
مساحت و محیط یک دایره با شعاعِ $r$ را با $p(r)$ و $s(r)$ نمایش دهید. پس $r$ متغیر ما و $p$ و $s$ دو تابع تکمتغیره بر حسب $r$ هستند. توجه کنید که پیش از معرفی انتگرال و مشتق و غیره، با مشاهده و آزمایش (کاری که فیزیک و شیمی و زیست و سایر دانشها امروز هم انجام میدهند) به این نتیجه رسیدند که $\frac{p(r)}{2r}$ و $\frac{s(r)}{r^2}$ برای هر $r$ای عدد ثابت میشوند و این دو عدد ثابت با هم برابر میشوند. این عدد ثابت را با $\pi$ نمایش دهید. اکنون از اینکه $\pi=\frac{p(r)}{2r}=\frac{s(r)}{r^2}$ چه نتیجهای میگیرید؟ $p(r)=2\pi r$ و $s(r)=\pi r^2$. از فیزیک به یاد آورید که $w=mg$ مثلا چگونه بدست آمدهاست؟ آیا ابتدا عدد $g$ بودهاست و سپس فرمولِ $w=mg$؟ آیا $g$ را بدون هیچ تعریفی ابتدا محاسبه کردند و سپس آمدهاند ثابت کردهاند $w=mg$ یا ابتدا دیدهاند $\frac{w}{m}$ ثابت است (با فرض ثابت بودن یک سری شرایط فیزیکی) و سپس آمدهاند $g$ را محاسبه کردهاند؟
اکنون ابزارهای بیشتری داریم که البته چیزی نیستند به جز همان ابزارهای قدیم ولی رابطههای بیشتری یافتهایم که چند محاسبهٔ طولانی را در زمان کوتاهتر انجام دهیم. در واقع زمانی که میگوئید $\int x\rm{d}x=\frac{1}{2}x^2$ چیزی به جز انجام دادن محاسبه کردن مساحت زیر یک سهگوش بدست آمده از سه خط محورهای مختصات و نیسماز یکچهارم یکم و سوم با کمک مستطیلهای داخل این سهگوش و سپس باریک و باریکتر کردن آنها و بیشتر کردن تعدادشان نیست. مقایسه کنید با فرمولها و نکتههای تستی که برای کنکور ممکن است حفظ کنید. به هر حال، حتی با داشتن انتگرال، اینطور نیست که عدد پی را ثابت کنیم! چه چیزی از یک عدد ثابت کردنی است؟ هنوز عدد پی معنایش همان نسبت محیط به قطر است. کاری که اکنون میتوانید انجام دهید این است که یکی از دو کسر پیشتر را به عنوان تعریف عدد $\pi$ بردارید و کسر دیگر را از آن نتیجه بگیرید.
تعریف: $\pi=\frac{p(r)}{2r}$. حکم: $\pi=\frac{s(r)}{r^2}$.
مانند شکل زیر یک دایره به شعاع $r$ بردارید، در این شکل شعاع ۱ گزیده شدهاست. آنگاه شعاعی از آن برداشته و به تعداد زیادی بخش بخشبندی کنید، در این شکل ۱۰ بخش مساوی که فاصلهٔ هر دو بخش $0.1$ است. دایرههای به مرکز یکسان ولی شعاع به اندازهٔ فاصلهٔ مرکز تا بخش مورد نظر بر روی شعاع را بکشید، در این شکل ۱۰ دایره داریم. مساحت دایرهٔ اصلی برابر با جمع مساحت نوارهای ایجاد شده بین این دایرهها است. فرض کنید بخشبندیها مساوی انجام شدهباشند، پس فاصلهٔ بین هر دو نوار در راستای یک شعاع برابر با یک عدد است، آن را $\Delta x$ نمایش دهید. در شکل ما $\Delta x=0.1$. مساحت نوار اگر فاصلهٔ محیط دایرهٔ بالاییاش تا مرکز دایره برابر با $x$ باشد تقریبا با مساحت مستطیل با پهنا (عرض) $\Delta x$ و درازای (طول) محیط دایرهٔ بالایی یعنی $p(x)=2\pi x$ برابر است. پس مساحت هر نوار را با $(2\pi x)\times \Delta x$ تقریب زدهایم و مساحت دایرهٔ اصلی را با جمع این مساحتها $\sum 2\pi x\Delta x$. با کوچکتر کردن $\Delta x$ و بیشتر کردن تعداد نوارها این جمع به انتگرال تبدیل میشود (حد یک دنباله از جمعها، یک سری).
\begin{align}
& s(r)=\int_0^r2\pi x\rm{d}x=2\pi\int_0^r x\rm{d}x=2\pi(\frac{1}{2}x^2\Big]_{x=0}^{x=r}=\pi r^2\\
& \Longrightarrow \frac{s(r)}{r^2}=\pi
\end{align}
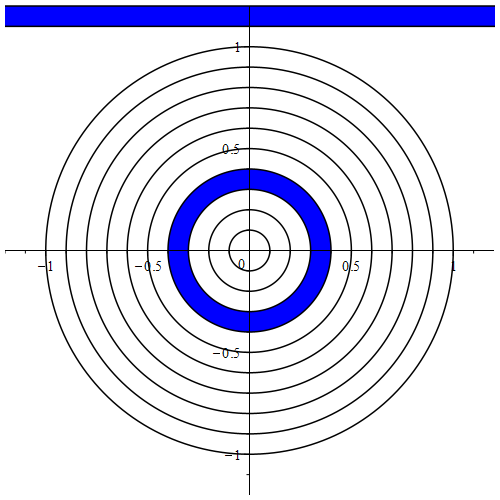
در شکل بالا نوار بین گردی (دایره) با پرتو (شعاع) $0.3$ و گردی با پرتوی $0.4$ با رنگ آبی نمایش داده شدهاست و مستطیلی که برای تقریب مساحت این نوار به کار گرفتهشدهاست نیز در بالای شکل کشیده و با رنگ آبی پر شدهاست.
اینک برویم سراغ رادیان! رادیان مانند سانتیگراد سلسیوس، متر، کلیوگرم، ثانیه یک واحد است. چگونه درجه برای زاویه تعریف میشد؟ میگفتید یک دایره رسم کنید و یک شعاع آن را ثابت بگیرید. محیط دایره را به ۳۶۰ بخش مساوی تقسیم کنید و این بخشبندی را از نقطهٔ برخورد این شعاعِ معیار با محیط دایره شروع کنید. اکنون هر خط دیگری که از مرکز این دایره بگذرد با خطی که از امتداد شعاعِ معیار ایجاد میشود در جهت پادساعتگرد یک زاویه میسازد. کمیت این زاویه را با شمارش تعداد بخشهای روی محیط این دایره که بین این دو خط با شروع از شعاع معیار تا محل برخورد خط جدید با محیط دایره هست تعیین میکنیم. غیر از این است؟ فرق اینچ با سانتیمتر چیست؟ در میزان معیار تقسیمبندی. اکنون رادیان چیست؟ به جای اینکه محیط دایره را ۳۶۰ بخش بکنیم، آن را $2\pi$ بخش میکنیم. این عدد صحیح نیست؟ خب نباشد. این عدد دقیقش را به اعشار تا انتها نداریم، خب نداشتهباشیم. زمانی که میگوئیم یک زاویه $\frac{\pi}{3}$ رادیان است، چگونه میتوانیم مقدارش را دقیق داشته باشیم وقتی $\pi$ صحیح یا گویا یا جبری نیست؟ مگر نیازی به این موردها داریم؟ یک دایرهٔ کامل $2\pi$، چقدر از یک دایره میشود $\frac{\pi}{3}$؟ یک نسبت و تناسب. یکششم یک دایرهٔ کامل. تمام.
آقا $\pi$ را از تساویهای دیگر هم میتوان بدست آورد، تناقضی نیست؟ مثلا $4\sum_{n=1}^\infty (-1)^{n+1}\frac{1}{2n-1}$. خب؟ چه تناقضی باید باشد؟ اگر دوست دارید، این را به عنوان تعریف بگیرید و سپس از آن به بقیهٔ تساویها برسید، این انتخاب خودتان است و تناقضی با هیچ چیزی ایجاد نمیکند. در پرسیدن پرسش باید دقت کنید، بد ادا کردن پرسش حتی باعث میشود خود پرسشکننده دچار سردرگمی و فراموش کردن پرسش اصلی و به جایش دچار ابهام و کجفهمی شود. یک پرسش معنادار اینجا این است که چگونه از تعریف $\pi$ بر اساس محیط دایره به چنین رابطهای میتوان رسید. این یک پرسش معنادار است. تابع $\tan$ را زمانی که درجهبندی زاویه بر حسب رادیان است در نظر بگیرید. بر اساس آن رابطهٔ وارون این تابع را بسازید که $\arctan$ است. اکنون $\arctan(1)=\frac{\pi}{4}$ یعنی چه؟ یعنی اینکه اگر زاویهمان یکهشتم زاویهٔ یک دایرهٔ کامل باشد، آنگاه $\tan$ برابر با یک میشود (امیدوارم تعریف تانژانت را متوجه شدهباشید). اکنون بسط تیلور این تابع را در $x=0$ بنویسید. سپس $x=1$ بگذارید. یک طرف که $\arctan(1)$ و در نتیجه $\frac{\pi}{4}$ میشود و طرف دیگر سری بالا بدون ضریب ۴. حالا برای یکی پرسش میشود که سری تیلور تابع $\arctan$ را چگونه باید بنویسیم؟ که پرسشی جدا است.