چیزی که در آخر باعث سردرگمی شما شدهبوداست استفادهٔ بیاعتبار از نمادهاست. خیلی ابتدایی از اولین برخورد با برابریها (معادلهها) در فرضا دبیرستان شروع میکنیم تا مشکل اصلی استفادهٔ نادرست از نمادها را در اینجا متوجه شویم. یک معادلهٔ یک متغیره یعنی یک عدد مجهول داریم که در تساویای صدق میکند و سپس میخواهیم مقدار مجهول را حدس بزنیم. مقدار مجهول را با یک نماد (فقط و فقط یک نماد) نمایش میدهیم مانند $x$. فرض کنید عددی که دوست شما در ذهنش گرفتهاش قرار است عددی حقیقی (دامنهٔ انتخابی برای متغیر) در برابری زیر صدق کند.
$$x-2=0$$
اکنون شما چون دامنهٔ تغییر متغیرتان اعداد حقیقی است از قانونهای حاکم بر میدان اعداد حقیقی و اعمالش استفاده میکنید تا معادله را حل کنید. در اینجا خیلی راحت از عمل دوتایی بودن جمع که تابع دومتغیره بودنش را میرساند استفاده میکنید. جمع یک تابع دو متغیره است. اینکه تابع باشد یعنی اگر دو ورودی یکسان بدهید دو خروجی یکسان دارید. ورودی برای یک تابع دومتغیره دو عدد است پس باید دو تا زوج مرتب یکسان بدهید و انتظار داشته باشید که دو تا عدد یکسان خروجی بگیرید. من دو زوج مرتب را اینها میگیرم، یک بار $(0,2)$ و یک بار دیگر $(x-2,2)$. توجه کنید که $x$ یک عدد است و در نتیجه $x-2$ نیز یک عدد است! پس حق داریم عمل جمع را بر روی زوج مرتب $(x-2,2)$ پیاده کنم. پس انتظار دارم که
$$(x-2)+2=0+2$$
سپس از شرکتپذیری عمل جمع استفاده میکنم که به من میگوید $(x-2)+2$ که همان $\big(x+(-2)\big)+2$ است برابر است با $x+\big((-2)+2\big)$ و سپس از عضو قرینهٔ جمعی استفاده میکنم که میگوید $(-2)+2=0$ پس سمت چپ عبارت بالایم تبدیل شد به $x+0$ اکنون نیز در هر دو سمت چپ و راست از عضو خنثای جمعی استفاده میکنم و میبینم که
$$x=2$$
مجهول ما یک عدد بود که مقدارش ۲ است و ما آن را با ویژگیهای میدان اعداد حقیقی یافتیم. اکنون یک گام بیشتر پیش برویم. فرض کنیم عددی که دوستمان در نظر گرفته است قرار است در معادلهٔ زیر صدق کند.
$$x^2-3x+2=0$$
این بار وارد همهٔ گامهای جزئی نمیشوم و فرض میکنم که گام زیر برایتان روشن است.
$$(x-1)(x-2)=0$$
بعد چه میشود؟ چیزی که میشود پریدن به تعریف نمادهای جدید نیست بلکه گامهای زیر را پیش میروم. میدانم که مجموعهٔ اعداد حقیقی همراه جمع و ضرب یک دامنهٔ صحیح است (در واقع میدان است و هر میدانی یک دامنهٔ صحیح است). دامنهٔ صحیح بودن به چه معنا بود؟ به این معنا بود که حاصلضرب هیچ دو عضو ناصفری (عضو خنثای جمعی) برابر با صفر نمیشود. پس از اینکه عددِ $x-1$ در عددِ $x-2$ ضرب شدهاست نتیجه میگیرم که حداقل یکی از این دوپ عدد باید صفر باشد، هر دو هم میتوانند صفر باشند، فعلا نمیدانیم چند تا از این دو عدد صفر هستند ولی حداقل یکیشان حتما باید باشد. پس نتیجهٔ کاملا منطقیِ زیر را داریم که از «یا»ی ریاضی (یای غیر مانع) استفاده میکند. یای نامانع یعنی اولی یا دومی یا هر دو. گاهی میبینید که از علامت هفتشکل مانندی برای نشان دادن یای ریاضی استفاده میکنند که در زیر ما نیز از این علامت استفاده کردهایم.
$$(x-1)(x-2)=0\Longrightarrow x-1=0\vee x-2=0$$
توجه کنید که علامتهای بدون تعریف و یکدفعهای مثل $x_1$ و $x_2$ به میان صفحه نیانداختهایم! نماد $x$ از ابتدای کار معرفی شد پس حق استفاده دارم، اگر حرف از نماد جدید بزنید باید ابتدا تعریف آن را بدهید. به هر حال جلو میرویم:
$$x-1=0\vee x-2=0\Longrightarrow x=1\vee x=2$$
چه شد؟ خب اول اینکه مشخص شد که هر دوی $x-1$ و $x-2$ نمیتوانستند هم زمان صفر شوند. و در آخر داریم که متغیر $x$ که فقط یک عدد است! میتواند یکی از دو عضو مجموعهٔ $\lbrace 1,2\rbrace$ باشد. هر یک از این دو در برابری صدق میکند. به هر عددی که در یک برابری صدق کند اصطلاحا یک ریشه برای آن برابری میگوئیم. برابری یکُم ما یک ریشه داشت. برابری جدیدمان دو ریشه دارد. الآن حق دارم بیایم و بگویم «تعریف میکنم $x_1$ عدد ۱ باشد و $x_2$ عدد ۲ و از الآن به بعد میتوانم از این دو نماد در ادامهٔ کارهایم استفاده کنم.».
یک گام دیگر پیش برویم. فرض کنیم عددی که دوستمان در ذهنش گرفته است عددی حقیقی است که در برابری زیر صدق کند.
$$x^4-1=0$$
با توجه به بحث باید محاسبهٔ زیر برایتان روشن باشد.
$$\begin{array}{rl}
x^4-1=0\Longrightarrow & (x^2-1)(x^2+1)=0\\
\Longrightarrow & \left\lbrace\begin{array}{l}
x^2-1=0\\
\vee\\
x^2+1=0
\end{array}\right.
\end{array}$$
چون $x^2+1=0$ روی اعداد حقیقی پاسخ ندارد پس $x^2+1=0\Longrightarrow x\in\emptyset$ و در مورد حالت دیگر $x^2-1=0\Longrightarrow x\in\lbrace 1,2\rbrace$ و چون در بینشان «یا» داشتیم داریم $x\in\emptyset\cup\lbrace 1,2\rbrace$ که میشود $x\in\lbrace 1,2\rbrace$ یا همان «$x$ میتواند ۱ یا ۲ باشد». اما فردی که نمادهای $x_1$ و $x_2$ و غیره بدون دلیل به کار میبرد اینطوری میشود که ما باید $x_1$ تا $x_4$ داشتهباشیم پس جوابهای سوم و چهارم کجا هستند؟ اگر همچین سوالی برایش پیش نیاید پس باید به او گفت که چگونه قبلا بدون اینکه این نمادها را تعریف کنید تعدادشان را میدانستید (دانستن تعداد نمادهایی که تعریف نشدهاند)! به هر حال پس اولین نکتهٔ مهم اول باید معادله را حل کنید، و سپس بعد از بدست آوردن ریشهها تعریف میکنید مثلا ریشهٔ اول را $\alpha$ مینامم و ریشهٔ دوم را $\beta$ مینامم یا مثلا همان نمادگذاری $x_1$ و $x_2$ و غیرهٔ خودتان. این نکتهٔ مهم اول برای شما. باز هم بیشتر پیش برویم.
فرض کنید عددی که در ذهن دوستتان است در برابری زیر صدق میکند.
$$x^2-x+\frac{3}{16}=0$$
اکنون چه کار میکنید؟ با چیزی که شما در متن پرسش انجام دادید اینجا هم میتواند فردی بیاید و بنویسد $x=x^2+\frac{3}{16}$ و سپس بگوید $x_1=x^2+\frac{3}{16}$ و حدس بزنید چه؟ بگوید برابری یک ریشه دارد که $x_1$ است و این ریشه چیست؟ و به هیجان بیافتد. مشکل اینجاست که این فرد فکر کرده است که حل کردن برابری یعنی رسیدن به چیزهایی که یک سمت تساوی $x$ است و حالا مهم نیست که آن طرف چه هست، هر چه باشد اسمش را ریشه یا جواب یا پاسخ میگذارد و از نمادهای $x_1$ و غیره استفاده میکند.
بیاییم بررسی کنیم چه اشکالهایی در کار این فرد وجود دارد.
- این فرد هنوز برابری را حل نکرده است.
- این فرد نماد $x_1$ را بدون تعریف قبلی وارد کار کردهاست.
- این فرد فکر میکند نوشتهٔ $x_1=x^2+\frac{1}{16}$ یک عدد است!
از مورد ۱ به ۳ شروع به درست کردن کار ایشان کنیم.
- بیایید برابری را حل کنیم. از روشهای زیادی میتوانید این کار را بکنید که آشنا هستید، استفاده از فرمول دلتا، استفاده از تجزیه، استفاده از روشهای عددی مانند حل عددی معادله بوسیلهٔ روش نیوتن، ... . در هر حال خواهیم داشت که $x\in\lbrace \frac{1}{4},\frac{3}{4}\rbrace$.
- این برابری تکریشهای نیست! دو ریشه دارد. اکنون میتواند بگوید بیاییم عدد $\frac{1}{4}$ را ریشهٔ اول با و با نماد $x_1$ نمایش دهید و عدد $\frac{3}{4}$ را ریشهٔ دوم و با نماد $x_2$ نمایش دهیم.
- آن عبارت $x_1=x^2+\frac{3}{16}$ چه معنایی میتوانست داشته باشد؟ معنایش ریشهٔ اول نیست، معنایش این است که $x$ هر چه هست، توان دویش را با سهشانزدهم جمع کنید آن چیز را $x_1$ مینامیم. پس در این حالت با فرض کردن اینکه هنوز $x$ همان معنای مجهول برابریمان را دارد، $x_1$ یک مجهول جدید است که مقدارهای ممکناش اعضای $\lbrace(\frac{1}{4})^2+\frac{3}{16},(\frac{3}{4})^2+\frac{3}{16}\rbrace$ است. که همان $\lbrace\frac{1}{4},\frac{3}{4}\rbrace$ است. اما مسلمان یک عدد نیست! ما یک متغیر جدید تعریف کردیم که مقادیرش برابر با مقادیر متغیر قبلیمان شد. در واقع معادله را به جای اینکه حل کنیم دوباره یک معادلهٔ جدید ساختیم. یعنی دستگاه تکمعادله-تکمجهول اصلی را تبدیل کردیم به دستگاه دو معادله-دومجهول زیر
$$\left\lbrace\begin{array}{l}
x^2-x+\frac{3}{16}=0\\
x_1-x^2-\frac{3}{16}=0
\end{array}\right.$$
که مجموعهٔ پاسخهای آن برابر است با $\lbrace(\frac{1}{4},\frac{1}{4}),(\frac{3}{4},\frac{3}{4})\rbrace$. و توجه کنید که فقط با داشتن برابری دوم نمیتوانید به این مجموعه پاسخ برسید. با فقط در نظر گرفتن $x_1=x^2+\frac{3}{16}$ به مجموعهنقاطی که خم زیر را در صفحهٔ دو بعدی $x\circ x_1$ میسازد میرسید!
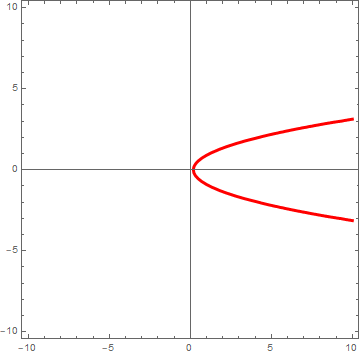
دستور رسم در نرمافزار Mathematica:
ContourPlot[x1==x^2+3/16,{x1,-10,10},{x,-10,10},Axes->True,ContourStyle->{Red,Thickness[0.01]}]
اکنون دیگر انتظار میرود که ابهامهای نمادین شما رفع شدهباشد. عبارت $x_1=\sqrt{14x}-7$ و دیگری در متن پرسش شما نه ۱) پاسخ، ریشه، حل، جواب برای معادلهتان هستند و نه ۲) عدد هستند. پس به طبع تناقض، ابهام یا ایهامی هم با داشتن یا نداشتن عدد موهومی در نوشتهشان نیز وجود ندارد.