این کلمه $n$ حرفی قرار است شامل $m$ عبارت $ab$ باشد . پس شکل کلی کلمه به صورت زیر است :
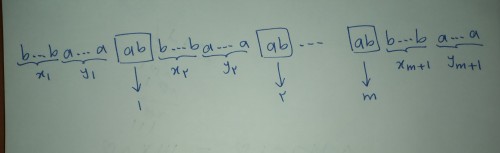
چون قرار است کلمه فقط حاوی $m$ عبارت $ab$ باشد پس قبل اولین عبارت $ab$ و بین هر دو عبارت متوالی $ab$ و بعد آخرین عبارت $ab$ نباید هیچ حرف $a$ قبل $b$ قرار گیرد. فرض کنید $ x_{k} $ و $ y_{k} $ ها به ترتیب تعداد حروف $b$ و $a$ در جایگاه های مشخص شده هستند پس :
$ x_{1} + y_{1} + x_{2} + y_{2} +...+ x_{m+1} + y_{m+1}=n-2m $
در این معادله $ x_{k} $ و $ y_{k} $ ها اعداد صحیح نامنفی هستند . پس تعداد این کلمات برابر است با تعداد جواب های معادله بالا در مجموعه اعداد صحیح نامنفی که برابر است با :
$$ \binom{(n-2m)+(2m+2)-1}{(2m+2)-1} = \binom{n+1}{2m+1} $$