ابتدا دامنه عبارت تابع را به دست میاوریم. اگر زبر رادیکال را بزرگتر مساوی صفر قرار دهید خواهید داشت:
$$-2\leq x\leq 0$$
حال محدوده x را داریم و میتوانیم عبارت داخل قدر مطلق را بسازیم. اگر به طرفین نامساوی ها عدد ۱ را اضافه کنیم عبارت داخل قدر مطلق ساخته میشود:
$$-1\leq x+1\leq1$$
خب برای این که بدانیم عبارت داخل قدر مطلق را چگونه از قدر مطلق خارج کنیم(خودش خارج شود یا قرینهاش) بازه به دست آمده را به دو بازه زیر میشکنیم و در هر بازه نمودار تابع را رسم میکنیم:
$$-1\leq x+1 <0$$
$$0\leq x+1 \leq1$$
خب حالا در هر بازه تابع را رسم میکنیم. در بازه اول چون عبارت داخل قدر مطلق منفی میشود پس قرینهاش از قدر مطلق خارج میشود. ضابطه تابع به صورت زیر میشود:
$$f(x)=\sqrt{x+2}$$
این نمودار را رسم میکنیم. شکل زیر:
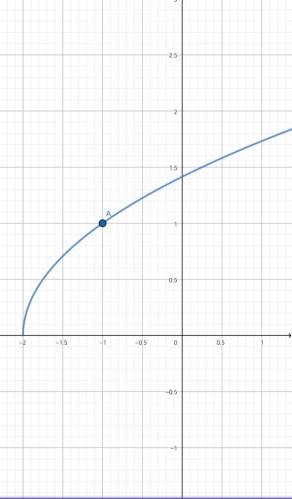
حال در بازه دوم نمودار را رسم میکنیم. ضابطه تابع به صورت زیر میشود:
$$f(x)=\sqrt{-x}$$
که به صورت زیر است:
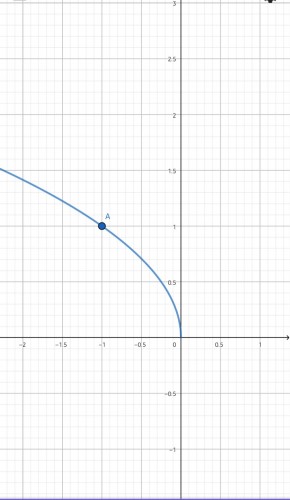
حال دو نمودار را در یک دستگاه رسم میکنیم. به برد و دامنه تابع اصلی دقت کنیم. نمودار به صورت زیر میشود:
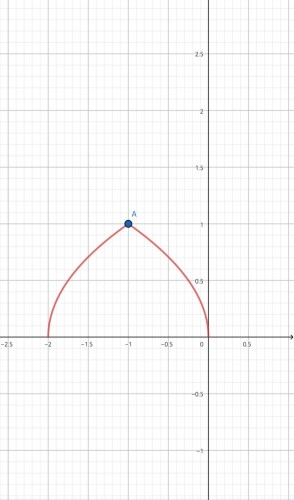
به دبیرتان هم بگوئید که در مرحله رسم $\sqrt{-x}$ و $\sqrt{x+2}$ از انتقال استفاده کردهاید. (: